Toplista
- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Pitagoras tétel
Brigi17
kérdése
713
Segítséget szeretnék kérni, a 7, 8, 9, 11, 18, 20 feladatok megoldásához.
Előre is nagyon köszönöm!!!!
Előre is nagyon köszönöm!!!!
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Középiskola / Matematika
Válaszok
6
VF
{ Informatikus }
megoldása
7.
`T = \frac{AM * BC}{2} = AM * BM = 105 cm^2`
`AM = \frac{105}{BM} = \frac{105}{7} = 15 cm`
`AB = \sqrt{AM^2 + BM^2} = \sqrt{15^2 + 7^2} = \sqrt{225 + 49} = \sqrt{274} = \color{red}16.552945 cm`
`T = \frac{AM * BC}{2} = AM * BM = 105 cm^2`
`AM = \frac{105}{BM} = \frac{105}{7} = 15 cm`
`AB = \sqrt{AM^2 + BM^2} = \sqrt{15^2 + 7^2} = \sqrt{225 + 49} = \sqrt{274} = \color{red}16.552945 cm`
0
- Még nem érkezett komment!
VF
{ Informatikus }
válasza
8.
`K = c * 4 = 40 cm^2`
`c = \frac{40}{4} = 10 cm`
`a^2 + b^2 = c^2`
`(2*b)^2 + b^2 = 10^2`
`2^2 * b^2 + b^2 = 10^2`
`4 * b^2 + b^2 = 100`
`5 * b^2 = 100`
`b^2 = \frac{100}{5} = 20`
`b = \sqrt{20} = 4.472136`
`a = 2 * b = 2 * 4.4721361 = 8.944272`
`T_{AOB} = \frac{a * b}{2} = \frac{4.472136 * 8.94427}{2} = \frac{40}{2} = 20 cm^2`
`T_{ABCD} = T_{AOB} * 4 = 20 * 4 = \color{red}80 cm^2`
`K = c * 4 = 40 cm^2`
`c = \frac{40}{4} = 10 cm`
`a^2 + b^2 = c^2`
`(2*b)^2 + b^2 = 10^2`
`2^2 * b^2 + b^2 = 10^2`
`4 * b^2 + b^2 = 100`
`5 * b^2 = 100`
`b^2 = \frac{100}{5} = 20`
`b = \sqrt{20} = 4.472136`
`a = 2 * b = 2 * 4.4721361 = 8.944272`
`T_{AOB} = \frac{a * b}{2} = \frac{4.472136 * 8.94427}{2} = \frac{40}{2} = 20 cm^2`
`T_{ABCD} = T_{AOB} * 4 = 20 * 4 = \color{red}80 cm^2`
0
-
VF: Ezt lehet túlbonyolítottam. Ezzel még várj, hátha valaki hozzászól. 2 éve 0
-
Brigi17: Köszönöm szépen a megoldásokat!!! 2 éve 0
VF
{ Informatikus }
válasza
9.
`FO = \sqrt{AF^2 - AO^2} = \sqrt{105^2 - 100^2} = \sqrt{11025 - 10000} = \sqrt{1025} \approx \color{red}32.015621`
`FO = \sqrt{AF^2 - AO^2} = \sqrt{105^2 - 100^2} = \sqrt{11025 - 10000} = \sqrt{1025} \approx \color{red}32.015621`
0
- Még nem érkezett komment!
VF
{ Informatikus }
válasza
11.
(Kissé furcsán hangzik, hogy dőlésnek nevezték a cm-ben megadandó eredményt, de szerintem erre gondoltak.)
`AF = \sqrt{DF^2 - AD^2} = \sqrt{26^2 - 24^2} = \sqrt{676 - 576} = \sqrt{100} = \color{red}10 cm`
Mivel a (10, 24, 26) pitagoraszi számok amelyekből kettőt már ismertünk, a harmadikat táblázatból is kikereshettük volna. Lásd: https://hu.wikipedia.org/wiki/Pitagoraszi_sz%C3%A1mh%C3%A1rmasok_list%C3%A1ja
(Kissé furcsán hangzik, hogy dőlésnek nevezték a cm-ben megadandó eredményt, de szerintem erre gondoltak.)
`AF = \sqrt{DF^2 - AD^2} = \sqrt{26^2 - 24^2} = \sqrt{676 - 576} = \sqrt{100} = \color{red}10 cm`
Mivel a (10, 24, 26) pitagoraszi számok amelyekből kettőt már ismertünk, a harmadikat táblázatból is kikereshettük volna. Lásd: https://hu.wikipedia.org/wiki/Pitagoraszi_sz%C3%A1mh%C3%A1rmasok_list%C3%A1ja
0
- Még nem érkezett komment!
VF
{ Informatikus }
válasza
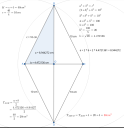
18.
`BE = \frac{AB - CD}{2} = \frac{36 - 20}{2} = \frac{16}{2} = 8 cm`
`AE = AB - BE = 28 cm`
`CE = \sqrt{BC^2 - BE^2} = \sqrt{10^2 - 8^2} = \sqrt{100 - 64} = \sqrt{36} = 6 cm`
`AC = \sqrt{AE^2 + CE^2} = \sqrt{28^2 + 6^2} = \sqrt{784 + 36} = \sqrt{820} \approx \color{red}28.635642 cm`
`BE = \frac{AB - CD}{2} = \frac{36 - 20}{2} = \frac{16}{2} = 8 cm`
`AE = AB - BE = 28 cm`
`CE = \sqrt{BC^2 - BE^2} = \sqrt{10^2 - 8^2} = \sqrt{100 - 64} = \sqrt{36} = 6 cm`
`AC = \sqrt{AE^2 + CE^2} = \sqrt{28^2 + 6^2} = \sqrt{784 + 36} = \sqrt{820} \approx \color{red}28.635642 cm`
0
- Még nem érkezett komment!
VF
{ Informatikus }
válasza
20.
`AO = \frac{AC}{2} = \frac{24}{2} = 12`
`BO = \sqrt{AB^2 - AO^2} = \sqrt{13^2 - 12^2} = \sqrt{169 - 144} = \sqrt{25} = 5`
`BD = BO * 2 = 5 * 2 = \color{red}10`
`AO = \frac{AC}{2} = \frac{24}{2} = 12`
`BO = \sqrt{AB^2 - AO^2} = \sqrt{13^2 - 12^2} = \sqrt{169 - 144} = \sqrt{25} = 5`
`BD = BO * 2 = 5 * 2 = \color{red}10`
0
- Még nem érkezett komment!