Kedves hallgatók! A portál oldalán azok közé a kevesek közé tartozom, aki "hibrid"
jelleggel megoldó is és egyúttal feladat kiíró is. Elismerem, hogy egyúttal túl lőttem
a célon, mert nem kifejezetten koordináta-geometria alkalmazásáról van szó.
Az az érzésem, hogy differenciálgeometria és az analízis alkalmazására is gondolni kell.

Ajánlom, hogy bontsuk a feladványt négy, de legalább három részre. Van egy "háromszögünk", ami
körül meg kellene oldani ezt a feladványt az `A(1; 1)`, `B(2; sqrt(2))` és `C(2; 4)` pontokkal.

Az első eset roppant egyszerűnek tűnik. Fektessünk egyeneseket az adott pontokra és
a kapott háromszögbe írható kör paramétereit keressük. Ez egy emelt szintű érettségi feladvány,
ezt illik mindenkinek megoldani. A második eset már nem annyira barátságos. `AC` egyenes egyenlete
`x mapsto 3x-2`, míg `BC` egyenes a triviális `x=2`. Az `AB` egyenes egyenletét cseréljük le a
`x mapsto sqrt(x)` egyenletű parabolára. És itt kéne elgondolkoznunk, hogy hogyan tovább.
Ez legyen a 2-es számú alfeladat.

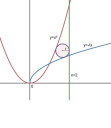
Ezek után térjünk vissza az eredeti feladathoz. Vegyük észre, hogy az `x mapsto x^2` és `x mapsto sqrt(x)` függvények
egymás inverzei. Ha a kérdéses kör az `P(x; x^2)` pontban érinti a piros színű parabolát, akkor
az ennek megfelelő inverz `Q(x^2; x)` pont is érintő pont lesz a másik az ábrán kék szinnel jelölt parabolán.
Legyen az érintő kör sugara `r` és így szimmetriaokokból a kör középpontja `O(2-r; 2-r)` lesz.
Nyilvánvaló, hogy a harmadik érintési pont az `x=2` egyenesen a `R(2; 2-r)` lesz.
Az `P` pontban a piros színű parabola érintőjének meredeksége `2x` lesz.
Az `PO` egyenes egyenletének felírásához alkalmazni fogjuk az egyenes normálvektoros egyenletét:
`frac{-(x-x_0)}{f'(x)}=y-y_0`. Vagyis `frac{x^2-2+r}{x-2+r}= frac{-1}{2x}`. Az `x` és `r` értékek közötti kapcsolatot
a kör egyenletének alkalmazásával is felírhatjuk:
`(x-2+r)^2+(x^2-2+r)^2=r^2`. Az előbbi egyenletből kifejezhetjük az `r`-t, így
`r=frac{2+3x-2x^3}{1+2x}`. Ezt behelyettesítve a kör egyenletébe kapjuk
a `frac{- (8·x^5 - 17·x^4 - 6·x^3 + 8·x^2 + 12·x + 4)}{(2·x + 1)^2}=0` egyenletet.
A tört számlálójában található polinom irreducibilis a racionális számok felett,
így az érintési pont koordinátái és a sugár ötödfokú algebrai számok.
Továbbá az érintési pont abcisszájára érvényes az `1 le x le 2` egyenlőtlenség.
Alkalmazható az egyik tanult közelítő módszer (Megjegyzés: A Newton-módszer `x_0=1,5` kezdő értékkel
és 7 lépéssel jó közelítést és gyors konvergenciát ad.) és így `x approx 1,332840...` és `r approx 0,344555...`.