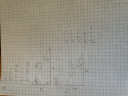Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Trigonometria
 kovacs07lili
kérdése
kovacs07lili
kérdése
279
Csatoltam a feladatot!
Jelenleg 1 felhasználó nézi ezt a kérdést.
matek, Matematika, trigonometria, szögfüggvény, háromszög, hegyesszögű
matek, Matematika, trigonometria, szögfüggvény, háromszög, hegyesszögű
0
Középiskola / Matematika
Válaszok
1 kazah
megoldása
kazah
megoldása
Gondolom most kezdtétek a szögfüggvényeket, így eleinte még nem sok tanulnivaló van, néhány alapvető gondolat.
Derékszögű háromszögekről van szó, az oldalak és a szögek közötti összefüggéseket tanuljátok.
A jelölésekhez ragaszkodj, a-val szemben `alpha`, b-vel szemben `beta`, c-vel szemben derékszög (90°).
Amit érdemes megtanulnod, az két-három összefüggés, plusz a sallangok, amire magadtól is rájössz.
1. Derékszögű háromszögben az adott szöggel szemközti befogó és az átfogó hányadosa a szög `color(red)("szinusz")`-a.
`sin alpha=a/c`
2. Derékszögű háromszögben az adott szög melletti befogó és az átfogó hányadosa a szög `color(blue)("koszinusz")`-a.
`cos alpha=b/c`
3. Derékszögű háromszőgben az adott szöggel szemközti befogó és a szög melletti befogó hányadosa a szög `color(green)("tangens")`-e.
`tan alpha=a/b`
4. Kotangens ennek a reciproka, azt már kitalálod.
Egyenlőre ennyi kell ahhoz, hogy az ilyen típusú feladatokat megoldd.
d,
Ha `beta`-t ismered és az átfogót, akkor ebből egyből akár a-t, akár b-t tudod számolni, felírod a megfelelő összefüggést, átalakítod és kiszámolod:
`sinbeta=b/c` `to` `b=c*sinbeta` = `16*sin54°12'`.
A szög itt fok-percben van megadva, érdemes átváltanod fokba (bár manapság vannak olyan számológépek, amibe be lehet vinni ilyen formában is, de jobb, ha tudod, hogyan kell).
Ugyanúgy váltod át, mint az óra-percet.
60 perc= 1 fok
12 perc = `12/60` = `1/5` = 0,2 fok.
tehát:
`b=16*sin54,2°` `approx` 12,98 m
Az a oldalt számolhatod Pitagorasz-tétellel vagy szögfüggvénnyel is (számold az egyikre, ellenőrizheted a másikra).
`cosbeta=a/c` `to` `a=c*cosbeta` = `16*cos54,2°` = 9,36 m
Ellenőrzés:
`a^2+b^2=c^2`
`9.36^2+12.98^2=16^2`
A derékszöghöz ne jelölj fokot, az biztosan 90°.
`alpha` kiszámítása nem hiszem, hogy gondot jelent, 90-ből kivonod a `beta`-t.
`alpha=90-beta` = `90-54.2` = 35,8° = 35°48'.
Visszaszámolni a fokot percre ugyanúgy.
1 fok = 60 perc
0,8 fok = `0.8*60` = 48 perc
e,
Ezt paraméteresen kell megoldanod, mivel nincsenek konkrét adatok megadva.
Adott c és `alpha`, itt alkalmazol egy szinuszt és egy koszinuszt és meg is vannak a hiányzó oldalak.
`sinalpha=a/c` `to` `a=c*sinalpha`
`cosalpha=b/c` `to` `b=c*cosalpha`
`beta=90-alpha`
Derékszögű háromszögekről van szó, az oldalak és a szögek közötti összefüggéseket tanuljátok.
A jelölésekhez ragaszkodj, a-val szemben `alpha`, b-vel szemben `beta`, c-vel szemben derékszög (90°).
Amit érdemes megtanulnod, az két-három összefüggés, plusz a sallangok, amire magadtól is rájössz.
1. Derékszögű háromszögben az adott szöggel szemközti befogó és az átfogó hányadosa a szög `color(red)("szinusz")`-a.
`sin alpha=a/c`
2. Derékszögű háromszögben az adott szög melletti befogó és az átfogó hányadosa a szög `color(blue)("koszinusz")`-a.
`cos alpha=b/c`
3. Derékszögű háromszőgben az adott szöggel szemközti befogó és a szög melletti befogó hányadosa a szög `color(green)("tangens")`-e.
`tan alpha=a/b`
4. Kotangens ennek a reciproka, azt már kitalálod.
Egyenlőre ennyi kell ahhoz, hogy az ilyen típusú feladatokat megoldd.
d,
Ha `beta`-t ismered és az átfogót, akkor ebből egyből akár a-t, akár b-t tudod számolni, felírod a megfelelő összefüggést, átalakítod és kiszámolod:
`sinbeta=b/c` `to` `b=c*sinbeta` = `16*sin54°12'`.
A szög itt fok-percben van megadva, érdemes átváltanod fokba (bár manapság vannak olyan számológépek, amibe be lehet vinni ilyen formában is, de jobb, ha tudod, hogyan kell).
Ugyanúgy váltod át, mint az óra-percet.
60 perc= 1 fok
12 perc = `12/60` = `1/5` = 0,2 fok.
tehát:
`b=16*sin54,2°` `approx` 12,98 m
Az a oldalt számolhatod Pitagorasz-tétellel vagy szögfüggvénnyel is (számold az egyikre, ellenőrizheted a másikra).
`cosbeta=a/c` `to` `a=c*cosbeta` = `16*cos54,2°` = 9,36 m
Ellenőrzés:
`a^2+b^2=c^2`
`9.36^2+12.98^2=16^2`
A derékszöghöz ne jelölj fokot, az biztosan 90°.
`alpha` kiszámítása nem hiszem, hogy gondot jelent, 90-ből kivonod a `beta`-t.
`alpha=90-beta` = `90-54.2` = 35,8° = 35°48'.
Visszaszámolni a fokot percre ugyanúgy.
1 fok = 60 perc
0,8 fok = `0.8*60` = 48 perc
e,
Ezt paraméteresen kell megoldanod, mivel nincsenek konkrét adatok megadva.
Adott c és `alpha`, itt alkalmazol egy szinuszt és egy koszinuszt és meg is vannak a hiányzó oldalak.
`sinalpha=a/c` `to` `a=c*sinalpha`
`cosalpha=b/c` `to` `b=c*cosalpha`
`beta=90-alpha`
0
- Még nem érkezett komment!