Paralelepipedon?

Itt a megoldás:

Ncore tavaszi kvíz 2024:

1, Egy mértani sorozat páros számú tagból áll. Ha minden elemét összeadjuk, az eredmény háromszor akkora lesz, mintha csak a páratlan sorszámúakat adjuk össze. Mekkora a sorozat hányadosa?


`S_n` = `a*(q^n-1)/(q-1)`

`S_m` = `a*((q^2)^(n/2)-1)/(q^2-1)`= `a*(q^n-1)/(q^2-1)`

Elosztod a két egyenletet egymással:

`S_n/S_m=((cancel((a*q^n-1))/(q-1))/(cancel((a*(q^n-1))/(q^2-1)` = `(q^2-1)/(q-1)` = `q+1=3`

A = `q=color(red)(2)`

2,

Három szám mértani sorozatot alkot, összegük 26. Ha az elsőhöz 1-et, a másodikhoz 6-ot, a harmadikhoz 3-at adunk, számtani sorozatot kapunk. Mekkora a három szám szorzata?

`a(1+q+q^2)=26` (Ez az első mondat)

`aq^2+3-aq-6=aq+6-a-1` (Ez meg a második, a szomszédos tagok különbsége egyenlő (állandó)).

`aq^2-2aq+a-8=0`

`a(q-1)^2=8`

`26(q-1)^2=8(1+q+q^2)`

`q_1=3` ; `q_2=1/3`

A mértani sorozat tagjait felcserélheted, így a mértani sorozat:

2,6,18 (vagy 18,6,2; `q=1/3` esetén)

A három szám szorzata pedig:

B = `2*6*18` = `color(red)("216")`.

3, Egy háromszög két oldala 4 cm és 5 cm, az általuk bezárt szög 45°. Mekkora a háromszög köré írható kör átmérője?


T = `4*5*sin45/2` = 7,071 cm^2 (A területet az adatok alapján tudod számolni).

Jöhet a koszinusztétellel a harmadik oldal hossza:

`c = root()(4^2+5^2-2*4*5*cos45)`= 3,566 cm

A köré írható kör átmérőjét ezzel a képlettel számolhatod:

C = `d=(abc)/(2T)`= `(4*5*3.566)/(2*7.071)` `approx` `color(red)("5 cm")`.

4,

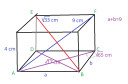
Egy egyenes paralelepipedon térátlói 9 cm és `root()(33)` cm; alapkerülete 18 cm, oldaléle 4 cm. Mekkora a térfogata?

Az egyenes paralelepipedon tulajdonképpen egy paralelogramma alapú hasáb.

Az oldalak a és b, a kerület `2*(a+b)=18` `to` a+b = 9 `to` b = 9-a

Ábra

A testátlókból kiszámoljuk a paralelogramma átlóit:

`bar(AC)` = `root()((root()(33))^2-4^2)` = `root()(17)` cm

`bar(BD)` = `root()(9^2-4^2)` = `root()(65)` cm

Felírjuk az átlók és az oldalak közötti összefüggéseket,melyekben szerepel(nek) a szög(ek) is.

ABC háromszög:

I. `(bar(AC))^2=a^2+(9-a)^2-2*a*(9-a)*cosgamma`

`17=a^2+(9-a)^2-2*a*(9-a)*cosgamma`

BCD háromszög:

II.: `(bar(BD))^2` = `a^2+(9-a)^2-2*a*(9-a)*cos(180-gamma)`

`65=a^2+(9-a)^2+2*a*(9-a)*cosgamma`

Összeadod a két egyenletet:

82=4a^2-36a+162

4a^2-36a+80=0

a^2-9a+20=0

a=4 ; b=5 vagy

a=5 ; b=4

`cosgamma` = `(4^2+5^2-17)/(2*4*5)` = 0,6

`singamma` = `root()(1-cos^2gamma)` = 0,8

D = `V=T*h` = `a*b*singamma*h` = `4*5*0.8*4` = `color(red)("64 " cm^3)`.

5, Egy sakkversenyen minden játékos pontosan egyszer játszott bármelyik másikkal. Összesen 171 játszmát játszottak. Hány versenyző volt?

Legyen 'a' játékos, akik játszottak mindenkivel, vagyis a-1 játékossal. `a*(a-1)` mérkőzés, ha oda-vissza játszanának, de csak 1 meccs volt mindenki ellen, így

`(a*(a-1))/2=171`

`a^2-a-342=0`

`a_(1,2)` = `(1 pm root()(1^2+4*342))/2` = `(1 pm 37)/2`

`a_1` = -18 játékos nem lehet.

E = `a_2` = `color(red)("19")` versenyző volt.

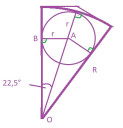
6, Egy 45°-os szögű körcikkből kivágható legnagyobb kör területe hány %-a a körcikk területének?

Ábra

Az OAB derékszögű háromszögben kifejezzük az OA szakaszt:

`bar(OA)`= `r/(sin22,5°)` `approx` 2,61r

r segítségével kifejezzük R-et:

R = `r+r/(sin22.5)` `approx` 3,61r

`T_1` = `r^2*pi`

A körcikk területe:

`T_2` = `R^2*pi/8` `approx` `(3.61r)^2*pi/8` `approx` `1.63r^2*pi`

F = `T_1/T_2*100` = `(r^2*pi)/(1.63*r^2*pi)*100` `approx` `color(red)("61")` (61,28)

7, Egy háromszög oldalai olyan mértani sorozatot alkotnak, melynek a hányadosa `q=4/3`. Mekkora a háromszög legnagyobb szöge?

Csak az oldalak aránya a lényeg, tehát választhatunk a-nak bármilyen értéket, legyen 1. Így az oldalak hossza:

`1`, `4/3`, `16/9`.

A koszinusztételt alkalmazzuk, a legnagyobb szög a leghosszabb oldallal szemben van.

`(16/9)^2=1^2+(4/3)^2-2*1*4/3*cosgamma`

`cosgamma=(1^2+(4/3)^2-(16/9)^2)/(2*1*4/3)` = -0,143

G = `gamma` = `color(red)("98°")`.

A beküldendő megoldás:

`X=14*(C*(A+B)+F*(D+E))/G` = `14*(5*(2+216)+61*(64+19))/98` = `ul(color(red)("879"))`.