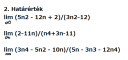Toplista
- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Határérték
Fruzsiiiiiiiiiiiiiii
kérdése
289
Segítenétek?
Addig eljutottam, hogy nyíllal felirkáltam milyen erős. Pl az ײ→2 x³→3 csak utána nem tudom hogyan tovább
Addig eljutottam, hogy nyíllal felirkáltam milyen erős. Pl az ײ→2 x³→3 csak utána nem tudom hogyan tovább
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Középiskola / Matematika
Válaszok
1
Bendigeidfran
{ Matematikus }
megoldása
Szia! Én ezt így csinálnám meg:
limx→∞5n²-12n+2)/(3n²-12)
Elosztjuk a változó legmagasabb hatványával, az n²-tel:
limx→∞5n²-12n+2)/(3n²-12)=5-12/n+2/n²)/(3-12/n²)
Ugye limx→af(x)/g(x)=limx→af(x)/limx→ag(x)
Tehát:
limx→∞5n²-12n+2)/(3n²-12)=limx→∞5-12/n+2/n²/limx→∞3-12/n²
A 12/n és a 2/n² valamint a 12/n² limitjei x→∞ esetében mind nulla felé mutatnak:
limx→∞5-12/n+2/n²/limx→∞3-12/n²=5-0+0/3-0=5/3
Ez lenne az első függvény limitje.
A következőt pontosan ugyan ezzel a módszerrel megcsinálva 0-t kell kapj.
Az utolsónál szintén ez a megoldás menete, ahol -1/4 kell kapj.
Remélem, tudtam segíteni!
limx→∞5n²-12n+2)/(3n²-12)
Elosztjuk a változó legmagasabb hatványával, az n²-tel:
limx→∞5n²-12n+2)/(3n²-12)=5-12/n+2/n²)/(3-12/n²)
Ugye limx→af(x)/g(x)=limx→af(x)/limx→ag(x)
Tehát:
limx→∞5n²-12n+2)/(3n²-12)=limx→∞5-12/n+2/n²/limx→∞3-12/n²
A 12/n és a 2/n² valamint a 12/n² limitjei x→∞ esetében mind nulla felé mutatnak:
limx→∞5-12/n+2/n²/limx→∞3-12/n²=5-0+0/3-0=5/3
Ez lenne az első függvény limitje.
A következőt pontosan ugyan ezzel a módszerrel megcsinálva 0-t kell kapj.
Az utolsónál szintén ez a megoldás menete, ahol -1/4 kell kapj.
Remélem, tudtam segíteni!
Módosítva: 2 éve
2
- Még nem érkezett komment!