Toplista
- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Matek geometria ABCD téglalap
janetmoovee88
kérdése
311
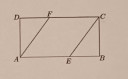
Az ABCD téglalap AB oldalának hossza 12cm, a BC oldal hossza 6cm. A téglalapba az AECF robuszt írjuk az ábrán látható módon (E az AB oldal, F a CD oldal egy pontja)
A) igazolja hogy a rombusz oldalainak hossza 7,5 cm
B) hány százaléka rombusz területe a téglalap területének?
A) igazolja hogy a rombusz oldalainak hossza 7,5 cm
B) hány százaléka rombusz területe a téglalap területének?
Jelenleg 1 felhasználó nézi ezt a kérdést.
Matek Geometria
Matek Geometria
0
Középiskola / Matematika
Válaszok
1
VF
{ Informatikus }
megoldása
A)
Behúzzuk a rombusz átlóit és a metszéspontjukat elnevezzük G-nek.
`AC = \sqrt{AB^2 + BC^2} = \sqrt{12^2 + 6^2} = \sqrt{144 + 36} = \sqrt{180} \approx 13.416408 cm`
`AG = AC // 2 = 13.416408 // 2 = 6.708204 cm`
`\hat{CAB} = arctan \frac{BC}{AB} = arctan \frac{6}{12} \approx 26.565051^o`
`EG = tan \hat{EAG} * AG = tan 26.565051 * 6.708204 \approx 3.354102 cm`
`AE = \sqrt{AG^2 + EG^2} = \sqrt{45 + 11.25} = \sqrt{56.25} = \color{red}7.5`
B)
`T_"téglalap" = AB * BC = 12 * 6 = 72 cm^2`
`T_"rombusz" = AE * BC = 7.5 * 6 = 45 cm^2`
Tehát a rombusz területe a téglalap területének `45 * 100 // 72 = color(red)62.5` százaléka.
Behúzzuk a rombusz átlóit és a metszéspontjukat elnevezzük G-nek.
`AC = \sqrt{AB^2 + BC^2} = \sqrt{12^2 + 6^2} = \sqrt{144 + 36} = \sqrt{180} \approx 13.416408 cm`
`AG = AC // 2 = 13.416408 // 2 = 6.708204 cm`
`\hat{CAB} = arctan \frac{BC}{AB} = arctan \frac{6}{12} \approx 26.565051^o`
`EG = tan \hat{EAG} * AG = tan 26.565051 * 6.708204 \approx 3.354102 cm`
`AE = \sqrt{AG^2 + EG^2} = \sqrt{45 + 11.25} = \sqrt{56.25} = \color{red}7.5`
B)
`T_"téglalap" = AB * BC = 12 * 6 = 72 cm^2`
`T_"rombusz" = AE * BC = 7.5 * 6 = 45 cm^2`
Tehát a rombusz területe a téglalap területének `45 * 100 // 72 = color(red)62.5` százaléka.
1
- Még nem érkezett komment!