Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Geometriai bizonyítás
 gyula205
kérdése
gyula205
kérdése
331
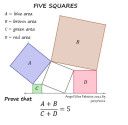
A pinterest-en találtam rá erre a feladatra. Bizonyítsuk be, hogy a négyzetek területe közötti összefüggést! A csatolmány forrása ez: https://hu.pinterest.com/pin/536983955588268138/
Jelenleg 1 felhasználó nézi ezt a kérdést.
geometria, bizonyítás
geometria, bizonyítás
0
Középiskola / Matematika
Válaszok
1 gyula205
válasza
gyula205
válasza
Ez egy emelt szintű érettségi feladat.
Helyezzük a koordináta-tengely origóját a fehér színű `a` oldalú négyzet jobb alsó sarok pontjába
és legyen ugyanennek a négyzetnek a dölése az x-tengelyhez képest `alpha`, ahol `0 le alpha le pi/2`.
Ekkor a `D` területű négyzet bal felső sarok pont koordinátái: `T(a*cos alpha; a*sin alpha)`. Ebben
a helyzetben (lásd a feladat ábráját) az `C` területű négyzet oldala `a*cos alpha` valmint a
`D` területű négyzet oldala `a*sin alpha` lesz. Így nyilvánvaló, hogy az `C+D=a^2`.
Be fogjuk látni, hogy `A+B=5*a^2`. Ehhez három pont koordinátáinak meghatározása
szükséges. A `D` területű négyzet jobb felső sarok pontja legyen `P`, az `a` oldalú fehér színű
négyzet legfelső sarokpontja legyen `Q` valamint a `C` területű négyzet bal felső sarok
pontja pedig `R`. Ekkor `P(a*(cos alpha+sin alpha); a*sin alpha)`,
`Q(a*(cos alpha-sin alpha); a*(cos alpha+sin alpha))` valamint `R(-a*(cos alpha+sin alpha); a*cos alpha)`.
A bizonyításhoz felvessszük még az `a` oldalú fehér színű négyzet bal felső sarokpontját.
Legyen ez az `S(-a*sin alpha; a*cos alpha)`. Mivel `vec(OT)`, `vec(OP)`, `vec(OQ)` és `vec(OR)` a választott koordináta-rendszer
helyvektorai, ezért `vec(OQ)=vec(OS)+vec(OT)`, amiből `Q` pont koordinátái meghatározhatók.
Az `vec(OP)=(a*sin alpha; 0)+vec(OT)` alapján kapjuk a `P` pont koordinátáit.
Az `vec(OR)=(-a*cos alpha; 0)+vec(OS)` alapján pedig az `R` pont koordinátáihoz férhetünk hozzá.
Végül `A+B=RP^2+PQ^2=(4a^2*cos^2 alpha+a^2sin^2 alpha)+(4a^2*sin^2 alpha+a^2*cos^2 alpha)=`
`=5a^2(sin^2 alpha+cos^2 alpha)=5a^2`.
Helyezzük a koordináta-tengely origóját a fehér színű `a` oldalú négyzet jobb alsó sarok pontjába
és legyen ugyanennek a négyzetnek a dölése az x-tengelyhez képest `alpha`, ahol `0 le alpha le pi/2`.
Ekkor a `D` területű négyzet bal felső sarok pont koordinátái: `T(a*cos alpha; a*sin alpha)`. Ebben
a helyzetben (lásd a feladat ábráját) az `C` területű négyzet oldala `a*cos alpha` valmint a
`D` területű négyzet oldala `a*sin alpha` lesz. Így nyilvánvaló, hogy az `C+D=a^2`.
Be fogjuk látni, hogy `A+B=5*a^2`. Ehhez három pont koordinátáinak meghatározása
szükséges. A `D` területű négyzet jobb felső sarok pontja legyen `P`, az `a` oldalú fehér színű
négyzet legfelső sarokpontja legyen `Q` valamint a `C` területű négyzet bal felső sarok
pontja pedig `R`. Ekkor `P(a*(cos alpha+sin alpha); a*sin alpha)`,
`Q(a*(cos alpha-sin alpha); a*(cos alpha+sin alpha))` valamint `R(-a*(cos alpha+sin alpha); a*cos alpha)`.
A bizonyításhoz felvessszük még az `a` oldalú fehér színű négyzet bal felső sarokpontját.
Legyen ez az `S(-a*sin alpha; a*cos alpha)`. Mivel `vec(OT)`, `vec(OP)`, `vec(OQ)` és `vec(OR)` a választott koordináta-rendszer
helyvektorai, ezért `vec(OQ)=vec(OS)+vec(OT)`, amiből `Q` pont koordinátái meghatározhatók.
Az `vec(OP)=(a*sin alpha; 0)+vec(OT)` alapján kapjuk a `P` pont koordinátáit.
Az `vec(OR)=(-a*cos alpha; 0)+vec(OS)` alapján pedig az `R` pont koordinátáihoz férhetünk hozzá.
Végül `A+B=RP^2+PQ^2=(4a^2*cos^2 alpha+a^2sin^2 alpha)+(4a^2*sin^2 alpha+a^2*cos^2 alpha)=`
`=5a^2(sin^2 alpha+cos^2 alpha)=5a^2`.
Módosítva: 1 éve
0
- Még nem érkezett komment!