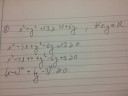Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Egyenlet
 Nagy István
kérdése
Nagy István
kérdése
446
Legyenek x, y valós számok! Melyik igaz az alábbi állítások közül?
1. ekkor x2 + y2 + 13 ≥ 4x + 6y mindig fennáll.
2. ekkor az x2 + y2 + 1 ≥ xy + x + y mindig fennáll.
1. ekkor x2 + y2 + 13 ≥ 4x + 6y mindig fennáll.
2. ekkor az x2 + y2 + 1 ≥ xy + x + y mindig fennáll.
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Középiskola / Matematika
Válaszok
4 bongolo
{
bongolo
{  }
válasza
}
válasza
1.
`x^2 + y^2 + 13 ≥ 4x + 6y`
Vigyük egyik oldalra az x-eket, másikra az y-okat:
`x^2 - 4x + 13 ≥ -y^2 + 6y`
Vonjunk ki mindkét oldalból 9-et... majd kiderül, miért jó ez
`x^2 - 4x + 4 ≥ -y^2 + 6y -9`
`x^2 - 4x + 4 ≥ -(y^2 - 6y + 9)`
Mindkét oldalon egy kifejezés négyzete van:
`(x-2)^2 ≥ -(y-3)^2`
Ez pedig minden valós számra igaz, mert a bal oldal sosem negatív, a jobb oldal pedig sosem pozitív.
`x^2 + y^2 + 13 ≥ 4x + 6y`
Vigyük egyik oldalra az x-eket, másikra az y-okat:
`x^2 - 4x + 13 ≥ -y^2 + 6y`
Vonjunk ki mindkét oldalból 9-et... majd kiderül, miért jó ez
`x^2 - 4x + 4 ≥ -y^2 + 6y -9`
`x^2 - 4x + 4 ≥ -(y^2 - 6y + 9)`
Mindkét oldalon egy kifejezés négyzete van:
`(x-2)^2 ≥ -(y-3)^2`
Ez pedig minden valós számra igaz, mert a bal oldal sosem negatív, a jobb oldal pedig sosem pozitív.
1
- Még nem érkezett komment!
 bongolo
{
bongolo
{  }
válasza
}
válasza
2.
`x^2 + y^2 + 1 ≥ xy + x + y `
`x^2 - xy - x + y^2-y+1 ≥ 0`
`x^2 - x(y+1) + (y^2-y+1) ≥ 0`
Teljes négyzetté alakítás:
Az első két tag ugyanaz, mint az `(x-(y+1)/2)` négyzete, hisz:
`(x-(y+1)/2)^2=x^2-x(y+1)+(y+1)^2/4`
Vagyis a kifejezés ennyi:
`(x-(y+1)/2)^2-(y+1)^2/4+ (y^2-y+1) ≥ 0`
`(x-(y+1)/2)^2+(4(y^2-y+1)-(y+1)^2)/4 ≥ 0`
Nézzük csak a második tört számlálóját:
`4(y^2-y+1)-(y+1)^2=4(y^2-y+1)-(y^2+2y+1)=`
`=3y^2-6y+3=3(y^2-2y+1)=3(y-1)^2`
Vagyis a teljes kifejezés:
`(x-(y+1)/2)^2+3/4(y-1)^2 ≥ 0`
Ez pedig minden valós x,y-ra igaz, hisz a négyzet nem lehet negatív.
`x^2 + y^2 + 1 ≥ xy + x + y `
`x^2 - xy - x + y^2-y+1 ≥ 0`
`x^2 - x(y+1) + (y^2-y+1) ≥ 0`
Teljes négyzetté alakítás:
Az első két tag ugyanaz, mint az `(x-(y+1)/2)` négyzete, hisz:
`(x-(y+1)/2)^2=x^2-x(y+1)+(y+1)^2/4`
Vagyis a kifejezés ennyi:
`(x-(y+1)/2)^2-(y+1)^2/4+ (y^2-y+1) ≥ 0`
`(x-(y+1)/2)^2+(4(y^2-y+1)-(y+1)^2)/4 ≥ 0`
Nézzük csak a második tört számlálóját:
`4(y^2-y+1)-(y+1)^2=4(y^2-y+1)-(y^2+2y+1)=`
`=3y^2-6y+3=3(y^2-2y+1)=3(y-1)^2`
Vagyis a teljes kifejezés:
`(x-(y+1)/2)^2+3/4(y-1)^2 ≥ 0`
Ez pedig minden valós x,y-ra igaz, hisz a négyzet nem lehet negatív.
1
- Még nem érkezett komment!
 gtamas99
{ Elismert }
válasza
gtamas99
{ Elismert }
válasza
Szia!
Amit bongolo leírt, természetesen teljesen helyes, én ennek ellenére leírom azt is, hogy én hogy csinálnám meg. Lényegében természetesen ugyanaz, de más a gondolatmenet.
Ilyenkor általában nullához viszonyítunk, mert valamiről könnyebb belátni, hogy pozitív-e vagy negatív, mint hogy mit tudom én milyen csúnyaságoknál kisebb vagy nagyobb. Hogy nullához viszonyítsak, vagy pozitív vagy negatív cuccokat kell kialakítsak a bal oldalon. Megsúgom, negatív cuccokat elég nehéz, ezért pozitívakat szoktunk kialakítani. És mi az, ami mindig pozitív? Egy teljes négyzet.
Vagyis teljes négyzeteket fogunk kialakítani. x2-4x, onnan jön az ötlet, hogy „ha ott még lenne egy plusz négy, akkor az pont (x-2)-nek a négyzete lenne”. Hasonlóan az y2-6y, oda egy kilences ha jönne, akkor pont (y-3)-nak a négyzetét látnám ott.
Ilyenkor legtöbbször a szabad taggal zsonglőrködsz. Azt szeded szét úgy, hogy neked jó legyen. Szerencsénkre most is ott van a szabad tag, a 13, ami (láss csodát ) pont szétszedhető mint 4+9.
) pont szétszedhető mint 4+9.
A 4-et írom az x-ekhez, a 9-et az y-okhoz, kialakítom a teljes négyzeteket.
Ekkor mondom, hogy (x-2)2 tuti pozitív, (y-3)2 hasonlóan, két pozitív szám összege pedig tuti pozitív, vagyis nagyobb mint nulla.
Három dolog, amit érdemes megjegyezni ilyen feladatokhoz. Vigyél át mindent az egyik oldalra, próbálj meg teljes négyzeteket kialakítani úgy, hogy a szabad tagot osztogatod szét, ahogy épp jó neked.
Amit bongolo leírt, természetesen teljesen helyes, én ennek ellenére leírom azt is, hogy én hogy csinálnám meg. Lényegében természetesen ugyanaz, de más a gondolatmenet.
Ilyenkor általában nullához viszonyítunk, mert valamiről könnyebb belátni, hogy pozitív-e vagy negatív, mint hogy mit tudom én milyen csúnyaságoknál kisebb vagy nagyobb. Hogy nullához viszonyítsak, vagy pozitív vagy negatív cuccokat kell kialakítsak a bal oldalon. Megsúgom, negatív cuccokat elég nehéz, ezért pozitívakat szoktunk kialakítani. És mi az, ami mindig pozitív? Egy teljes négyzet.
Vagyis teljes négyzeteket fogunk kialakítani. x2-4x, onnan jön az ötlet, hogy „ha ott még lenne egy plusz négy, akkor az pont (x-2)-nek a négyzete lenne”. Hasonlóan az y2-6y, oda egy kilences ha jönne, akkor pont (y-3)-nak a négyzetét látnám ott.
Ilyenkor legtöbbször a szabad taggal zsonglőrködsz. Azt szeded szét úgy, hogy neked jó legyen. Szerencsénkre most is ott van a szabad tag, a 13, ami (láss csodát
 ) pont szétszedhető mint 4+9.
) pont szétszedhető mint 4+9. A 4-et írom az x-ekhez, a 9-et az y-okhoz, kialakítom a teljes négyzeteket.
Ekkor mondom, hogy (x-2)2 tuti pozitív, (y-3)2 hasonlóan, két pozitív szám összege pedig tuti pozitív, vagyis nagyobb mint nulla.
Három dolog, amit érdemes megjegyezni ilyen feladatokhoz. Vigyél át mindent az egyik oldalra, próbálj meg teljes négyzeteket kialakítani úgy, hogy a szabad tagot osztogatod szét, ahogy épp jó neked.
1
- Még nem érkezett komment!
 Rantnad
{
Rantnad
{  }
megoldása
}
megoldása
Ha Brute Force-módszerrel akarjuk megoldani, akkor pakoljunk mindenkit át a bal oldalra:
x² - 4x + y² - 6y + 13 ≥ 0
Erre az egyenlőtlenségre tekintsünk úgy, mint egy másodfokú parametrikus egyenlőtlenségre, ahol ha x az ismeretlen, akkor y a paraméter, tehát az y²-6y+13-at egy-az-egyben konstansnak tekintjük. Erre írjuk fel a másodfokú megoldóképletet:
x1;2 = (4±√ 16-4*1*(y²-6y+13) )/(2*1). Most arra vagyunk kíváncsiak, hogy a gyökjel alatti rész lehet-e pozitív, mert ha igen, akkor két gyöke van a kifejezésnek, vagyis valahol mindenképp felvesz negatív értéket, vagyis mi akkor járunk jól, hogyha mindenhol negatív értéket vesz fel:
16-4*1*(y²-6y+13)≤0, ezt már meg tudjuk oldani, és azt látjuk, hogy az y=3-at kivéve, ahol 0-t vesz fel, mindenhol negatív az érték. Tehát a fenti egyenlőtlenségnek legfeljebb 1 gyöke lehet, és mivel az x² előjele pozitív, így mindenhol pozitív értéket vesz fel, illetve y=3 esetén lesz egyszer 0.
A második is kijön ezzel a módszerrel:
x² - (y+1)*x + y² - y + 1 ≥ 0, erre is felírjuk a megoldóképletet:
x1;2 = y+1±√ (y+1)²-4*1*(y²-y+1) /(2*1), itt is a gyökjel alatti résznek kell legfeljebb 0-nak lennie:
(y+1)²-4*1*(y²-y+1) ≤ 0, és erre azt kapjuk, hogy az y=1-et kivéve mindenhol negatív lesz az érték, tehát az eredeti egyenlőtlenségnek legfeljebb 1 gyöke lehet, és itt is x² együtthatója pozitív, ezért mindenhol pozitív értéket vesz fel, egyedül y=1 esetén lesz valahol 0.
(Természetesen az elemi lépéseket használó megoldások sokkal elegánsabbak, ellenben nem feltétlenül működik az ilyenfajta sakkozás mindig, ez viszont minden (polinomiális) esetre használható.)
x² - 4x + y² - 6y + 13 ≥ 0
Erre az egyenlőtlenségre tekintsünk úgy, mint egy másodfokú parametrikus egyenlőtlenségre, ahol ha x az ismeretlen, akkor y a paraméter, tehát az y²-6y+13-at egy-az-egyben konstansnak tekintjük. Erre írjuk fel a másodfokú megoldóképletet:
x1;2 = (4±√ 16-4*1*(y²-6y+13) )/(2*1). Most arra vagyunk kíváncsiak, hogy a gyökjel alatti rész lehet-e pozitív, mert ha igen, akkor két gyöke van a kifejezésnek, vagyis valahol mindenképp felvesz negatív értéket, vagyis mi akkor járunk jól, hogyha mindenhol negatív értéket vesz fel:
16-4*1*(y²-6y+13)≤0, ezt már meg tudjuk oldani, és azt látjuk, hogy az y=3-at kivéve, ahol 0-t vesz fel, mindenhol negatív az érték. Tehát a fenti egyenlőtlenségnek legfeljebb 1 gyöke lehet, és mivel az x² előjele pozitív, így mindenhol pozitív értéket vesz fel, illetve y=3 esetén lesz egyszer 0.
A második is kijön ezzel a módszerrel:
x² - (y+1)*x + y² - y + 1 ≥ 0, erre is felírjuk a megoldóképletet:
x1;2 = y+1±√ (y+1)²-4*1*(y²-y+1) /(2*1), itt is a gyökjel alatti résznek kell legfeljebb 0-nak lennie:
(y+1)²-4*1*(y²-y+1) ≤ 0, és erre azt kapjuk, hogy az y=1-et kivéve mindenhol negatív lesz az érték, tehát az eredeti egyenlőtlenségnek legfeljebb 1 gyöke lehet, és itt is x² együtthatója pozitív, ezért mindenhol pozitív értéket vesz fel, egyedül y=1 esetén lesz valahol 0.
(Természetesen az elemi lépéseket használó megoldások sokkal elegánsabbak, ellenben nem feltétlenül működik az ilyenfajta sakkozás mindig, ez viszont minden (polinomiális) esetre használható.)
2
- Még nem érkezett komment!