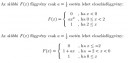Toplista
- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Igaz?
kapesmate
kérdése
645
A következő állítások közül melyik igaz/hamis?
Szerintem első hamis, mert az a=0-ra is eloszlásfüggvény...ellenben azért gondolom ,hogy a második igaz, mert akkor már a=0-nál nem lenne balról folytonos. Rosszul gondolom?
Szerintem első hamis, mert az a=0-ra is eloszlásfüggvény...ellenben azért gondolom ,hogy a második igaz, mert akkor már a=0-nál nem lenne balról folytonos. Rosszul gondolom?
Jelenleg 1 felhasználó nézi ezt a kérdést.
matek, valszám, eloszlás, függvény, balról, folytonos, végtelen, 1, határérték, Valószínűség
matek, valszám, eloszlás, függvény, balról, folytonos, végtelen, 1, határérték, Valószínűség
0
Felsőoktatás / Matematika
Válaszok
2
kapesmate
válasza
Az eloszlásfüggvény azt a definícióját használom, ahol F(x)=P(X<x) tehát nincs megengedve az egyenlőség...
0
- Még nem érkezett komment!
bongolo
{ 
}
megoldása
Attól függ, hogyan definiáltátok az eloszlásfüggvényt.
a) F(x)=P(ξ ≤ x) ez szokott lenni a definíció az angol nyelvű irodalomban
b) F(x)=P(ξ < x) ez meg a magyarban
Az a) esetben jobbról folytonos, a b) esetben balról folytonos az eloszlásfüggvény.
Ilyen a jobbról folytonos: https://upload.wikimedia.org/wikipedia/commons/thumb/7/77/Dis_Uniform_distribution_CDF.svg/1280px-Dis_Uniform_distribution_CDF.svg.png
Ilyen meg a balról folytonos: http://rs1.szif.hu/~szorenyi/elm/image282.gif
A feladatban az első függvény a=1/4 esetén mindenhol folytonos, más esetben pedig x=2-ban jobbról folytonos. Vagyis ez az a) definíció esetén minden nem-negatív a-nál lehet eloszlásfüggvény. Viszont a b) definíció esetén csak a=1/4-nél jó, mert balról nem folytonos egyébként.
A második függvény a=1/2-nél folytonos, más esetekben x=-2-nél balról folytonos, x=0-nál jobbról folytonos, tehát egyik definícióval sem lehet eloszlásfüggvény.
Az a gyanúm, hogy az a) definíciót tanulhattátok, tehát jobbról folytonosság az igény.
... most látom, hogy írtad, hogy a b) definíciót tanultátok. Akkor mindkettő igaz. De úgy nem annyira izgalmas a feladat
a) F(x)=P(ξ ≤ x) ez szokott lenni a definíció az angol nyelvű irodalomban
b) F(x)=P(ξ < x) ez meg a magyarban
Az a) esetben jobbról folytonos, a b) esetben balról folytonos az eloszlásfüggvény.
Ilyen a jobbról folytonos: https://upload.wikimedia.org/wikipedia/commons/thumb/7/77/Dis_Uniform_distribution_CDF.svg/1280px-Dis_Uniform_distribution_CDF.svg.png
Ilyen meg a balról folytonos: http://rs1.szif.hu/~szorenyi/elm/image282.gif
A feladatban az első függvény a=1/4 esetén mindenhol folytonos, más esetben pedig x=2-ban jobbról folytonos. Vagyis ez az a) definíció esetén minden nem-negatív a-nál lehet eloszlásfüggvény. Viszont a b) definíció esetén csak a=1/4-nél jó, mert balról nem folytonos egyébként.
A második függvény a=1/2-nél folytonos, más esetekben x=-2-nél balról folytonos, x=0-nál jobbról folytonos, tehát egyik definícióval sem lehet eloszlásfüggvény.
Az a gyanúm, hogy az a) definíciót tanulhattátok, tehát jobbról folytonosság az igény.
... most látom, hogy írtad, hogy a b) definíciót tanultátok. Akkor mindkettő igaz. De úgy nem annyira izgalmas a feladat
Módosítva: 7 éve
1
-
kapesmate: Köszönöm!
7 éve
0