Question

Középszintű matek

bacsa.istvan72 { Kérdező } kérdése

215 1 éve

Köszi

Jelenleg 1 felhasználó nézi ezt a kérdést.

0

Középiskola / Matematika

Válaszok

2

Ármós Csaba válasza

1 éve

Csatoltam képet.

0

**kazah** megoldása · Accepted Answer · 2023-11-26 19:42:45

a,

$lg(root(3)(x))*log_x 1000=lg x^2 +lg(1/x)$

$x gt 0$ ;

$x ne 1$

$1/3*lgx*log_x 1000=2*lgx+(-lgx)$

$1/3*lgx*log_x 1000=lgx$ /: lgx

$1/3*log_x 1000=1$ /*3

$log_x 1000 = 3$

$x^3=1000$

x = 10

$in$ É. T.

I: {10}

b,

$3||5-x|-6| le 9$

I. Ha

$x ge 5$

$3|x-5-6| le 9$

$3|x-11| le 9$

I. a:

Ha

$5 le x le 11$ :

$3(11-x) le 9$

$33-3x le 9$

$x ge 8$

$in$ É. T (tehát 8 és 11 között szóba jöhet).

I. b,

Ha

$x ge 11$

$3(x-11) le 9$

$3x-33 le 9$

$x le 14$

$in$ É.T. (11 és 14 között is jó).

II. ha

$x le 5$

$3|(5-x)-6| le 9$

$3|-1-x| le 9$

II. a

Ha

$x ge -1$

$3(x+1) le 9$

$3x+3 le 9$

$x le 2$ (-1 és 2 között)

II. b

Ha

$x le -1$

$3(-1-x) le 9$

$-3-3x le 9$

$x ge -4$ (-4 és -1 között)

Mind a 4 tartományban volt megoldás, összegezve:

$x in RR$ ;

$x in [-4;2]cup[8;14]$

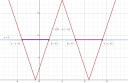
Ábra

c,

I.

$xy(x+y)=12$

II.

$(x+y)(x^2-xy+y^2)=28$

I. *3 :

$3x^2y+3xy^2=36$

+ II.

$x^3+3x^2y+3xy^2+y^3=36+28$

$(x+y)^3=64$

$x+y=4$

I:

$4*x*y=12$

$xy=3$

$x(4-x)=3$

$x^2-4x+3=0$

$(x-1)(x-3)=0$

$x_1=1$

$to$

$y_1=3$

$x_2=3$

$to$

$y_2=1$

Keresés

Toplista

Középszintű matek

Válaszok