a)
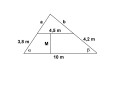
Lásd az ábrát.

Felrajzoltam a vasúti töltés keresztmetszetét, ami egy trapéz, és beírtam az adatokat.

A trapéz kiegészíthető egy háromszöggé az ábra szerint.

Ez azért jó nekünk, mert így két hasonló háromszöget kapunk: Az 'a' és 'b' és 4,5 oldalú háromszög hasonló az a+3,8 és b+4,2 és 10 oldalú háromszöghöz.

Így alkalmazhatjuk a párhuzamos szelők tételét:
a/(a+3,8) = 4,5/10
10a = 4,5a + 3,8*4,5
5,5a = 3,8*4,5
a=(3,8*4,5)/5,5 = 3,11 méter

b/(b+4,2) = 4,5/10
10b = 4,5b + 4,2*4,5
5,5b = 4,2*4,5
b=(4,2*4,5)/5,5 = 3,44

A nagy háromszög oldalai:
3,8+a = 6,91 méter
4,2+b = 7,64 méter
és 10 méter meg van adva.

A koszinusz tétellel ki tudjuk számolni a háromszög oldalaiból az α és β szöget:

7,64² = 6,91² + 10² - 2*6,91*10*cos α
cos α = 0,6467
α = 49,7⁰

6,91² = 7,64² + 10² - 2*7,64*10* cos β
cos β = 0,7240
β = 43,6⁰

b)
Innen már megvan a trapéz magassága (M), mert M merőleges a 10 méteres alapra, így írhatjuk, hogy
sin α = M/3,8
M=3,8*sin α = 3,8* sin 49,7⁰ = 2,9 méter

c)
A terület pedig:
T = (10+4,5)*M/2 (tehát a kisalap+nagyalap szorozva magasság/2)
T=14,5*2,9/2 = 21 m²