Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Szöggfüggvény
 Zitazagyvai
{ Kérdező } kérdése
Zitazagyvai
{ Kérdező } kérdése
824
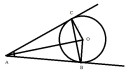
Egy 15 cm sugarú körhöz egy külső P pontból érintőket húzunk. Az érintők hajlásszöge 38 fok 46' Mekkora távolságra van a P pont a kör középpontjától? Mekkorák az érintő szakaszok és mekkora az érintési pontok távolsága?
Rajzzal!
Rajzzal!
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Középiskola / Matematika
Válaszok
2 csettlik
megoldása
csettlik
megoldása
A P és O pontot összekötő szakasz egyben az érintési egyenesek hajlásszögének felezője.
Az érintő és az érintési pontba húzott sugár derékszöget zár be.
`sinα="szöggel szembeni befogó"/"átfogó"` Ezt átrendezve:
`"átfogó"="szöggel szembeni befogó"/sinα`
Helyettesítsünk be:
`"átfogó"=(15/2)/sin((38°46')/2)`
`"átfogó"=22","60(cm)`
A Pitagorasz tétellel kiszámolhatod a érintő szakaszok hosszát (`a^2+b^2=c^2` segítségével)
De a fenti számolást át is írhatjuk a következőre:
`cosα="szög melletti befogó"/"átfogó"` átrendezve: `cosα*"átfogó"="szög melletti befogó"`
`cos((38°46')/2)*22","60="szög melletti befogó"`
`"szög melletti befogó"=21","32(cm)`
A két érintési pont távolsága a következőképpen számolható:
Maradjunk az ismert dolgok mellett. Ismerjük az érintési pont és P pont távolságát: `21","32(cm)`, ismerjük az érintők hajlásszögét, sőt ismerjük ennek a szögnek a felét is. Keressük a magasságot, ami éppen az érintési pontok távolságának a fele lesz.
Tehát a derékszögű háromszögben ismerjük az egyik szöget, valamint a hosszabb befogót és keressük a szöggel szembeni befogót.
Ismerjük fel a képletet:
`sinα="szöggel szembeni befogó"/"átfogó"` rendezzük át
`sinα*"átfogó"="szöggel szembeni befogó"`
`sin((38°46')/2)*21","32="szöggel szembeni befogó"`
`"szöggel szembeni befogó"=7","08(cm)`
Bocs lemaradt a két pont távolsága `14","16(cm)`
Az érintő és az érintési pontba húzott sugár derékszöget zár be.
`sinα="szöggel szembeni befogó"/"átfogó"` Ezt átrendezve:
`"átfogó"="szöggel szembeni befogó"/sinα`
Helyettesítsünk be:
`"átfogó"=(15/2)/sin((38°46')/2)`
`"átfogó"=22","60(cm)`
A Pitagorasz tétellel kiszámolhatod a érintő szakaszok hosszát (`a^2+b^2=c^2` segítségével)
De a fenti számolást át is írhatjuk a következőre:
`cosα="szög melletti befogó"/"átfogó"` átrendezve: `cosα*"átfogó"="szög melletti befogó"`
`cos((38°46')/2)*22","60="szög melletti befogó"`
`"szög melletti befogó"=21","32(cm)`
A két érintési pont távolsága a következőképpen számolható:
Maradjunk az ismert dolgok mellett. Ismerjük az érintési pont és P pont távolságát: `21","32(cm)`, ismerjük az érintők hajlásszögét, sőt ismerjük ennek a szögnek a felét is. Keressük a magasságot, ami éppen az érintési pontok távolságának a fele lesz.
Tehát a derékszögű háromszögben ismerjük az egyik szöget, valamint a hosszabb befogót és keressük a szöggel szembeni befogót.
Ismerjük fel a képletet:
`sinα="szöggel szembeni befogó"/"átfogó"` rendezzük át
`sinα*"átfogó"="szöggel szembeni befogó"`
`sin((38°46')/2)*21","32="szöggel szembeni befogó"`
`"szöggel szembeni befogó"=7","08(cm)`
Bocs lemaradt a két pont távolsága `14","16(cm)`
Módosítva: 2 éve
0
-
Zitazagyvai: és a rajz? 2 éve 0
-
csettlik: Oh, kérlek. Az is lemaradt.
 2 éve
0
2 éve
0