Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Szöggfüggvény
 Zitazagyvai
{ Kérdező } kérdése
Zitazagyvai
{ Kérdező } kérdése
839
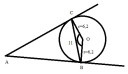
Egy körhöz érintőket húzunk egy külső pontból, a kör sugara 6,2 cm és az érin- tési pontokat összekötő szakasz hossza 11 cm. Mekkora az érintők hajlásszöge? Mekkora az érintőszakaszok hossza? Rajzzal!
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Középiskola / Matematika
Válaszok
1 csettlik
megoldása
csettlik
megoldása
Mellékeltem ábrád, hogy könnyebb legyen.
Kétféleképpen is meg lehet oldani a feladatot.
1. Szinusz segítségével
Az ábrán látható ABOD deltoid. Ebből a ismerjük az egyik átlóját.
Az ABO háromszögben, ha behúzzuk az O csúcshoz a szögfelezőt, ami egyben a háromszög magassága is, akkor lesz egy olyan derékszögű háromszögünk, aminek két oldalát ismerjük és az egyik szögét keressük.
`sinα="szöggel szembeni befogó"/"átfogó"`
`sinα=(11/2)/(6","2)=62","51°`
Az eredményünk csak az O csúcsnál lévő félszög. Ebből az következik, hogy O-nál lévő szög: `125","02°`
A deltoidra is igaz, hogy a belső szögeinek összege `360°`. A kör érintője és a kör sugara derékszöget zár be, így már tudjuk is, az érintők hajlásszöge: `360°-2*90°-125","02°=54","98°`
2. Koszinusz tétel használatával (már ha tanultátok)
Egy bármilyen háromszögben a koszinusz tétel a következő:
`c^2=a^2+b^2-2*a*b*cosγ`
Ha a feladatra lefordítjuk, akkor a BOC háromszögben ismerjük a három oldalt és keressük a legnagyobb szöget:
`11^2=6","2^2+6","2^2-2*6","2*6","2*cosγ` `cosγ`-ra rendezve
`cosγ=-(11^2-2*6","2^2)/(2*6","2^2)=-0","574`
`γ=125","02°`
Innen már ugyan az igaz, mint az előző megoldásnál.
Kétféleképpen is meg lehet oldani a feladatot.
1. Szinusz segítségével
Az ábrán látható ABOD deltoid. Ebből a ismerjük az egyik átlóját.
Az ABO háromszögben, ha behúzzuk az O csúcshoz a szögfelezőt, ami egyben a háromszög magassága is, akkor lesz egy olyan derékszögű háromszögünk, aminek két oldalát ismerjük és az egyik szögét keressük.
`sinα="szöggel szembeni befogó"/"átfogó"`
`sinα=(11/2)/(6","2)=62","51°`
Az eredményünk csak az O csúcsnál lévő félszög. Ebből az következik, hogy O-nál lévő szög: `125","02°`
A deltoidra is igaz, hogy a belső szögeinek összege `360°`. A kör érintője és a kör sugara derékszöget zár be, így már tudjuk is, az érintők hajlásszöge: `360°-2*90°-125","02°=54","98°`
2. Koszinusz tétel használatával (már ha tanultátok)
Egy bármilyen háromszögben a koszinusz tétel a következő:
`c^2=a^2+b^2-2*a*b*cosγ`
Ha a feladatra lefordítjuk, akkor a BOC háromszögben ismerjük a három oldalt és keressük a legnagyobb szöget:
`11^2=6","2^2+6","2^2-2*6","2*6","2*cosγ` `cosγ`-ra rendezve
`cosγ=-(11^2-2*6","2^2)/(2*6","2^2)=-0","574`
`γ=125","02°`
Innen már ugyan az igaz, mint az előző megoldásnál.
Módosítva: 2 éve
0
- Még nem érkezett komment!