A kotangens a legkönnyebb, mert az a tangens reciproka, tehát 4.

A többire két lehetőséget is mutatok:

1. Csinálhatjuk tisztán algebrai módszerrel: a tangens a szinusz és a koszinusz hányadosa, tehát `sinx/cosx=1/4`, vagyis `cosx=4sinx`. Ha ezt négyzetre emeljük, és kihasználjuk, hogy `sin^2x+cos^2x=1`, akkor előbb-utóbb kijön. (De figyelni kell arra, hogy a négyzetre emelés nem ekvivalens átalakítás, mert az előjeleket eleszítjük, tehát azokat még külön meg kell vizsgálni.)


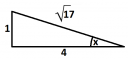
2. Sokkal egyszerűbb viszont a tangens geometriai értelmezésére visszavezetni a dolgot. Rajzolj egy derékszögű háromszöget, amelynek a két befogója 1 és 4 hosszúságú. Ekkor az 1 hosszú befogóval szemközti szög mértéke `x`. A Pitagorasz-tétel alapján az átfogó `sqrt(1^2+4^2)=sqrt(17)`. Innen már fel tudjuk írni a többi szögfüggvényt: `sinx=1/sqrt(17)` és `cosx=4/sqrt(17)`. Sajnos viszont még nem vagyunk kész, mert a tangens nem csak hegyesszögekre van értelmezve, hanem periodikus, azaz ha `tanx=1/4`, akkor `tan(x+k*pi)=1/4` szintén. `pi` radiánonként a szinusz és a koszinusz előjelet váltogatnak, tehát `sinx=-1/sqrt(17)` és `cos(x)=-4/sqrt(17)` is lehet.