Toplista
- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Függvény
Nagy István
kérdése
525
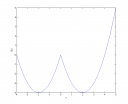
Adott az f: [–4;5] → R, f(x)=x²-4IxI függvény. Határozzuk meg a függvény minimumát!
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Középiskola / Matematika
Válaszok
1
AlBundy
{ Polihisztor }
megoldása
Vizsgáljuk meg a függvényt az értelmezési tartomány negatív és pozitív felén külön-külön!
A [-4;0] intervallumon `f(x)=x^2+4x=(x+2)^2-4`. Tehát az `x=-2` helyen van egy lokális minimum, amelynek az értéke `-4`.
A [0;5] intervallumon `f(x)=x^2-4x=(x-2)^2-4`. Tehát az `x=2` helyen van egy lokális minimum, amelynek az értéke `-4`.
A két lokális minimum megegyezik, tehát a válasz az, hogy a függvény minimuma -4, és ezt két helyen is felveszi.
A [-4;0] intervallumon `f(x)=x^2+4x=(x+2)^2-4`. Tehát az `x=-2` helyen van egy lokális minimum, amelynek az értéke `-4`.
A [0;5] intervallumon `f(x)=x^2-4x=(x-2)^2-4`. Tehát az `x=2` helyen van egy lokális minimum, amelynek az értéke `-4`.
A két lokális minimum megegyezik, tehát a válasz az, hogy a függvény minimuma -4, és ezt két helyen is felveszi.
Módosítva: 8 éve
1
- Még nem érkezett komment!