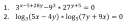Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Egyenletrendszer
 Törölt
kérdése
Törölt
kérdése
268
Oldja meg az alábbi egyenletrendszert!
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Középiskola / Matematika
Válaszok
1 RationalRick
{ Fizikus }
válasza
RationalRick
{ Fizikus }
válasza
`{(3^(x-5+28y)-9^3*27^(y+5)=0), (log_3(5x-4y)*log_5(7y+9x)=0):}`
Először a felsővel foglalkozom:
`3^(x-5+28y)-9^3*27^(y+5)=0`
`3^(x-5+28y)=3^6*3^(3(y+5))`
`3^(x-5+28y)=3^(3y+21)`
az exponenciális függvény szigorú monotonitása miatt:
`x-5+28y=3y+21`
`x=-25y+26`
Beírom a másikba:
`log_3(5(-25y+26)-4y)*log_5(7y+9(-25y+26))=0`
`log_3(-129y+130)*log_5(-218y+234)=0`
kikötés:
`-129y+130>0`
`y<(130)/(129)`
és
`-218y+234>0`
`y<(117)/(109)`
`D=]-∞, (130)/(129) [`
egy szorzat akkor nulla, ha az egyik tényezője nulla
`log_3(-129y+130)=0`
`log_3(-129y+130)=log_(3)1`
a logaritmusfüggvény szigorú monotonitása miatt:
`-129y+130=1`
`y=1` `inD`
`log_5(-218y+234)=0`
`log_5(-218y+234)=log_(5)1`
a logaritmusfüggvény szigorú monotonitása miatt:
`-218y+234=1`
`y=(233)/(218)` `∉D`
`color(blue)(y=1)`
`x=-25*2+26=1`
Ellenőrzés:
`3^(1-5+28*1)-9^3*27^(1+5)=3^(24)-3^(24)=0=0`
`log_3(5*1-4*1)*log_5(7*1+9*1)=log_(3)1*log_(5)16=0*16=0=0`
`M={(1, 1)}`
Először a felsővel foglalkozom:
`3^(x-5+28y)-9^3*27^(y+5)=0`
`3^(x-5+28y)=3^6*3^(3(y+5))`
`3^(x-5+28y)=3^(3y+21)`
az exponenciális függvény szigorú monotonitása miatt:
`x-5+28y=3y+21`
`x=-25y+26`
Beírom a másikba:
`log_3(5(-25y+26)-4y)*log_5(7y+9(-25y+26))=0`
`log_3(-129y+130)*log_5(-218y+234)=0`
kikötés:
`-129y+130>0`
`y<(130)/(129)`
és
`-218y+234>0`
`y<(117)/(109)`
`D=]-∞, (130)/(129) [`
egy szorzat akkor nulla, ha az egyik tényezője nulla
`log_3(-129y+130)=0`
`log_3(-129y+130)=log_(3)1`
a logaritmusfüggvény szigorú monotonitása miatt:
`-129y+130=1`
`y=1` `inD`
`log_5(-218y+234)=0`
`log_5(-218y+234)=log_(5)1`
a logaritmusfüggvény szigorú monotonitása miatt:
`-218y+234=1`
`y=(233)/(218)` `∉D`
`color(blue)(y=1)`
`x=-25*2+26=1`
Ellenőrzés:
`3^(1-5+28*1)-9^3*27^(1+5)=3^(24)-3^(24)=0=0`
`log_3(5*1-4*1)*log_5(7*1+9*1)=log_(3)1*log_(5)16=0*16=0=0`
`M={(1, 1)}`
Módosítva: 2 éve
0
-
Törölt: Az első az log3 nem log5. 2 éve 0
-
RationalRick: Ó, tényleg. De a lényegen nem változtat semmit, ugyanez lesz a megoldás 2 éve 0
-
RationalRick: Javítottam 2 éve 0