Egyenlet

`e)`

`(x-2)/(x+2)>=(2x-3)/(4x-1)`

kikötés:

`x+2≠0`
`x≠-2`

`4x-1≠0`
`x≠1/4`

`D=RR\\{0; 1/4}`

`(x-2)/(x+2)>=(2x-3)/(4x-1)`

`(x-2)/(x+2)-(2x-3)/(4x-1)>=0`

`((x-2)(4x-1)-(2x-3)(x+2))/((x+2)(4x-1))>=0`

`(4x^2-8x-x+2-2x^2+3x-4x+6)/(4x^2-x+8x-2)>=0`

`(2x^2-10x+8)/(4x^2+7x-2)>=0`

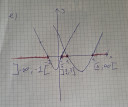
Ezt innen grafikusan a legkönnyebb megoldani szerintem.

zérushelyek:

`2x^2-10x+8=0`

`x_1=1`
`x_2=4`

`4x^2+7x-2=0`

`x_1=-2`
`x_2=1/4`

Ezt az utóbbi kettőt egyrészt a kikötés miatt nem veheti fel, másrészt pedig azért mert a nevező nem lehet nulla. A számláló viszont lehet, mert `>=` jel van.

A grafikonról csatolom a képet.

`M=]-∞, -2[cup]1/4, 1]cup[4, ∞[`

`f)`

`3-(2x-17)/(x-5)>(x-5)/(x+2)`

kikötés:

`x-5≠0`
`x≠5`

`x+2≠0`
`x≠-2`

`D=RR\\{-2; 0}`

`3-(2x-17)/(x-5)>(x-5)/(x+2)`

`3-(2x-17)/(x-5)-(x-5)/(x+2)>0`

`(3(x-5)(x+2)-(2x-17)(x+2)-(x-5)^2)/((x-5)(x+2))>0`

`(3x^2+6x-15x-30-2x^2+13x+34-x^2+10x-25)/(x^2-3x-10)>0`

`(14x-21)/(x^2-3x-10)>0`

zérushelyek:

`14x-21=0`

`x=3/2`

`x^2-3x-10=0`

`x_1=-2`
`x_2=5`

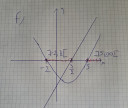
A grafikonról csatolom a képet.

`M=]-2, 3/2[cup]5, ∞[`