Egyenlőtlenség

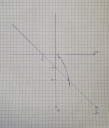
A legegyszerűbb a grafikus megoldás:

ábrázoljuk az x-4 egyenest egy x-y koordináta rendszerben, és ábrázoljuk a √2x-et is ugyanitt.

Pár érték behelyettesítésével: a √2x nullából indul, a gyökjel alatt nem lehet negatív szám a valós számok halmazán: x∈R és x≥0 a feltétel.

A √2x 0-nál 0, 2-nél 2-t, 8-nál 4-et vesz fel. Ez lesz a fél parabola.

Az x-4 meredeksége +1, és -4-nél metszi az y tengelyt.

A kettő ott egyenlő, ahol metszik egymást.
Az egyenes ott kisebb, mint a görbe, ahol az egyenes a görbe alatt fut (ott vesz fel kisebb értékeket).

Tehát a megoldás:
x≥0 és x≤8 esetén lesz x-4≤√2x

Így is írhatjuk: 0≤x≤8

Ennél a feladatnál specifikusan valóban a grafikus megoldás a legegyszerűbb, viszont az algebrai megoldással sem olyan nehéz és általában gyorsabb is.
Az egyetlen dolog, amire oda kell figyelni, hogy x∈R+, azaz x csak a pozitív valós számok halmazán vehet fel értéket. Innentől már csak meg kell oldani az egyenlőtlenséget, úgy, mintha egy egyenlet lenne, akár képlettel is.

x-4 ≤ √2x - Négyzetre emeljük mindkét oldalt
(x-4)² ≤ 2x - Itt fellelhető egy azonosság: (a-b)²=a²-2ab+b²
x²-8x+16 ≤ 2x -Nullára rendezzük az egyenlőtlenséget
x²-10x+16 ≤ 0 -Jelen esetben szorzattá tudjuk alakítani a kifejezést
(x-8)(x-2) ≤ 0 -Itt már ki is rajzolódik a két gyökünk, a 2, illetve a 8, tehát az egyenlőtlenség megoldása:
x∈ ]-∞,2[ ∪ ]-∞,8[ ⇒ x∈ ]-∞,8[
Viszont az elején kikötöttük, hogy x∈R+, azaz x nem vehet fel negatív értéket.
Ezért a végleges megoldás:
x∈ ]0,8[, azaz 0≤x≤8 - Ezek után behelyettesítve 8-cal és 0-val világossá válik a megoldás helyessége
Amennyiben hamar észreveszed az összefüggéseket, ez a módszer sokkal gyorsabb, mint a grafikus megoldás, valamint megfelelő odafigyeléssel és ellenőrzéssel olykor biztosabb megoldás is lehet. Ha tényleg biztosra akar menni az ember, akkor a hagyományos ellenőrzés után, az algebrai megoldást le lehet ellenőrizni grafikus módszerrel.