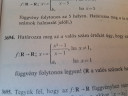Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Határérték számítás, folytonosság
 Fruzsiiiiiiiiiiiiiii
kérdése
Fruzsiiiiiiiiiiiiiii
kérdése
333
Az 3678 3679 és 3684es feladatra lenne szükségem.
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Középiskola / Matematika
Válaszok
1 kazah
megoldása
kazah
megoldása
`(x^3-6x^2)/(x^4-6x^3)` = `(cancel(x^2)*cancel((x-6)))/(cancel(x^2)*x*cancel((x-6)))` = `1/x`
A 0 helyen tehát nincs véges határértéke, az x=6 helyen `f(6)=1/6`, tehát van.
3679,
`(x^2+4x+3)/(x+3)` = `((x+1)cancel((x+3)))/cancel((x+3))` = `x+1`
Az x=-3 helyen a függvény határértéke `f(-3)=-3+1=-2`
3684 nincs
3694,
`(x^3-1)/(x-1)` = `(cancel((x-1))(x^2+x+1))/cancel((x-1))` = `x^2+x+1`
A függvény akkor lesz folytonos az x=1 helyen, ha
`a=f(1)=1^2+1+1=color(red)("3")` értéket adjuk neki.
0
-
Fruzsiiiiiiiiiiiiiii: Köszönöm! 2 éve 0
-
Fruzsiiiiiiiiiiiiiii: Igen a 94-esre gondoltam bocsánat 2 éve 0