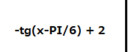Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Szinusz, koszinusz tangens függvény
 Fruzsiiiiiiiiiiiiiii
kérdése
Fruzsiiiiiiiiiiiiiii
kérdése
299
A 3 függvény ábràzolásának menetében szeretnék segítséget kérni illetve a jellemzésben.
A jellemzéshez csatolok mintát hogy nekem mit kell tudnom megállapítani róla. A π-s részekhez is szükségem lenne magyarázatra , mert mindig belegabalyodom hogy mi a menete.
Előre is köszönöm!
A jellemzéshez csatolok mintát hogy nekem mit kell tudnom megállapítani róla. A π-s részekhez is szükségem lenne magyarázatra , mert mindig belegabalyodom hogy mi a menete.
Előre is köszönöm!
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Középiskola / Matematika
Válaszok
1 kazah
megoldása
kazah
megoldása
Mindig induljunk ki az alapfüggvényekből.
Periódus: szinusz, koszinusz esetén `2pi`, tangens esetén `pi`.
Ha eltolások vannak, akár a belső függvénnyel, akár kívül, azzal a periódus nem változik.
Ha nyújtás, zsugorítás, akkor
- a külső függvény esetén (pl. 2cosx) a periódus nem változik.
- ha a függvény argumentumában van szorzás/osztás, akkor annak megfelelően ellentétesen történik a periódus változása (itt most nincs olyan példa, tehát mindegyiknél marad a `2pi` és a `pi`, viszont pl. `sin(2x)` esetén `(2pi)/2=pi` lesz a periódus).
- minimum-maximum:
Hely: Az eltolással annak megfelelően változnak a helyek és az értékek.
Példa:
- a sinx függvénynek a maximumai a `(pi/2+2k pi;1)` ; minimumai `((3pi)/2+2k*pi;1)`
A `sin(x+pi)-2` ehhez képest: az első koordináta `pi`-vel balra ; a második koordináta 2-vel fel. Tehát:
- Az új maximum `((3pi)/2+2k*pi; 3)` ; az új minimum `(pi/2+2k*pi;3)`
Értelemszerűen ugyanennyivel tolódik el a konvex tartomány is (az első koordináták vannak feltüntetve nálad, így csak azokat kell eltolnod).
`2*cosx+1`
A belső függvény nem változik, így a periódusa sem (`2*k*pi`).
A minimuma a koszinuszfüggvénynek `pi+2*k*pi;-1` , a maximuma `2*k*pi;1`
A függvénytranszformációk során történt egy nyújtás, majd egy eltolás az y tengely mentén, így a helyek (első koordináták) nem változnak, az értékek pedig a kétszeresére nőnek + eggyel nőnek.
Az új minimumok: `(pi+2*k*pi;-1)` ; az új maximumok: `(2*k*pi;3)`
`sin(x+pi)-2`
A periódusa ugyanannyi, mint az alapfüggvénynek, a függvény argumentumán belül nincs változás. (`2pi`).
Szélsőértékek:
Az alapfüggvény minimuma `(3pi)/2+2*k*pi;-1` ; maximuma `pi/2+2*k*pi;1)`
A függvény `pi`-vel el van tolva negatív irányba és az y tengely mentén pozitív irányba 2 egységgel, így az új szélsőértékek:
Minimum: `(pi/2+2*k*pi;1)` ; Maximum: `((3pi)/2+2*k*pi;3)`
A monotonitás a minimumtól maximumig növekvő; a maximumtól minimumig csökkenő.
Ha értelmezési tartomány is kell:
A szinusz-koszinusznál `x in RR`, ez nem változik.
Tangens esetében `x in RR, x ne pi/2+k*pi` az alapfüggvényé. Ha történt eltolás a függvény argumentumában, akkor annyival megy ellentétes irányba, ahol nem értelmezzük a függvényt.
Értékkészlet:
szinusz-koszinusz esetén az alapfüggvény [-1;1], ha volt nyújtás, akkor annyiszorosa (a külső függvényt, tehát pl `2*cosx`), illetve ha eltolva lett a függvény valamennyivel, akkor annyival változik az értékkészlet.
tangens esetén bármilyen érték lehet.
Nagyjából ennyi.
Periódus: szinusz, koszinusz esetén `2pi`, tangens esetén `pi`.
Ha eltolások vannak, akár a belső függvénnyel, akár kívül, azzal a periódus nem változik.
Ha nyújtás, zsugorítás, akkor
- a külső függvény esetén (pl. 2cosx) a periódus nem változik.
- ha a függvény argumentumában van szorzás/osztás, akkor annak megfelelően ellentétesen történik a periódus változása (itt most nincs olyan példa, tehát mindegyiknél marad a `2pi` és a `pi`, viszont pl. `sin(2x)` esetén `(2pi)/2=pi` lesz a periódus).
- minimum-maximum:
Hely: Az eltolással annak megfelelően változnak a helyek és az értékek.
Példa:
- a sinx függvénynek a maximumai a `(pi/2+2k pi;1)` ; minimumai `((3pi)/2+2k*pi;1)`
A `sin(x+pi)-2` ehhez képest: az első koordináta `pi`-vel balra ; a második koordináta 2-vel fel. Tehát:
- Az új maximum `((3pi)/2+2k*pi; 3)` ; az új minimum `(pi/2+2k*pi;3)`
Értelemszerűen ugyanennyivel tolódik el a konvex tartomány is (az első koordináták vannak feltüntetve nálad, így csak azokat kell eltolnod).
`2*cosx+1`
A belső függvény nem változik, így a periódusa sem (`2*k*pi`).
A minimuma a koszinuszfüggvénynek `pi+2*k*pi;-1` , a maximuma `2*k*pi;1`
A függvénytranszformációk során történt egy nyújtás, majd egy eltolás az y tengely mentén, így a helyek (első koordináták) nem változnak, az értékek pedig a kétszeresére nőnek + eggyel nőnek.
Az új minimumok: `(pi+2*k*pi;-1)` ; az új maximumok: `(2*k*pi;3)`
`sin(x+pi)-2`
A periódusa ugyanannyi, mint az alapfüggvénynek, a függvény argumentumán belül nincs változás. (`2pi`).
Szélsőértékek:
Az alapfüggvény minimuma `(3pi)/2+2*k*pi;-1` ; maximuma `pi/2+2*k*pi;1)`
A függvény `pi`-vel el van tolva negatív irányba és az y tengely mentén pozitív irányba 2 egységgel, így az új szélsőértékek:
Minimum: `(pi/2+2*k*pi;1)` ; Maximum: `((3pi)/2+2*k*pi;3)`
A monotonitás a minimumtól maximumig növekvő; a maximumtól minimumig csökkenő.
Ha értelmezési tartomány is kell:
A szinusz-koszinusznál `x in RR`, ez nem változik.
Tangens esetében `x in RR, x ne pi/2+k*pi` az alapfüggvényé. Ha történt eltolás a függvény argumentumában, akkor annyival megy ellentétes irányba, ahol nem értelmezzük a függvényt.
Értékkészlet:
szinusz-koszinusz esetén az alapfüggvény [-1;1], ha volt nyújtás, akkor annyiszorosa (a külső függvényt, tehát pl `2*cosx`), illetve ha eltolva lett a függvény valamennyivel, akkor annyival változik az értékkészlet.
tangens esetén bármilyen érték lehet.
Nagyjából ennyi.
0
-
Fruzsiiiiiiiiiiiiiii: Köszönöm 2 éve 0
-
kazah: Szívesen 2 éve 0