Toplista
- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Pótvizsga feladat
Kassai-Dávid
kérdése
265
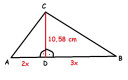
Egy derékszögű háromszög magasságvonala 10,58 cm hosszú, mely 2:3 arányban osztja fel az átfogót. Számítsd ki a derékszögű háromszög területét és köré írható körének kerületét!
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Középiskola / Matematika
Válaszok
1
kazah
válasza
Ábra
A két belső háromszög (ACD és BCD) hasonló, a megfelelő oldalak aránya egyenlő.
`(2x)/10.58=10.58/(3x)`
`6x^2=10.58^2`
`x=root()(10.58^2/6)` `approx` 4,32 cm
A köré írható kör átmérője a nagy háromszög átfogója.
d = 5x = `5*4.32` = 21,6 cm
K = `pi*d` = `3.14*21.6` = 67,8 cm
A háromszög területe az átfogó és a magasság szorzatának fele:
`T_h=(d*m)/2` = `(21.6*10.58)/2` = 114,3 `cm^2`
A két belső háromszög (ACD és BCD) hasonló, a megfelelő oldalak aránya egyenlő.
`(2x)/10.58=10.58/(3x)`
`6x^2=10.58^2`
`x=root()(10.58^2/6)` `approx` 4,32 cm
A köré írható kör átmérője a nagy háromszög átfogója.
d = 5x = `5*4.32` = 21,6 cm
K = `pi*d` = `3.14*21.6` = 67,8 cm
A háromszög területe az átfogó és a magasság szorzatának fele:
`T_h=(d*m)/2` = `(21.6*10.58)/2` = 114,3 `cm^2`
0
- Még nem érkezett komment!