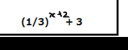Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Exponenciális és logaritmus függvény
 Fruzsiiiiiiiiiiiiiii
kérdése
Fruzsiiiiiiiiiiiiiii
kérdése
395
Ennek a 3 függvénynek az ábrázolásában szeretnék segítséget kérni. Nem igazán látom át az ábrazolás menetét. Nagyon nagy segítség lenne, ha valaki elmagyarázná.
Előre is köszönöm a segítséget!
Előre is köszönöm a segítséget!
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Középiskola / Matematika
Válaszok
1 kazah
megoldása
kazah
megoldása
`4^(x-1)-2`
1. Először ábrázolod az alapfüggvényt, az `4^x` lesz. Az exponenciális függvényeknek két alapesete van, ha az alap egynél nagyobb, akkor szigorúan monoton növekvő, ha egynél kisebb (0 és 1 közötti), akkor szigorúan monoton csökkenő.
A függvényábrázolások alapesetei:
- A függvény argumentumában végezzük el a műveletet (x helyett x-1 lesz a kitevőben). Ilyenkor az x tengely mentén történik az eltolás, ellentétes előjellel, mint a feltüntetett művelet. A mi konkrét példánkban itt eltolás történik 1 egységgel pozitív irányba.
- A függvény argumentumán kívül történik a transzformáció, (itt kivonunk kettőt az exponenciális kifejezésből). Ekkor eltolás történik, csak az y tengely mentén, megegyező előjellel. A konkrét példában 2 egységgel negatív irányba.
- Lehet még tükrözés abban az esetben, ha szorzunk -1-gyel, vagy eléteszünk egy mínusz jelet. (ha lesz ilyen, majd mutatom)
- Nyújtás, zsugorítás. A függvényt szorozzuk, osztjuk valamilyen valós számmal. (később, ha lesz ilyen)
Ha nem akarod mindegyik függvényt ábrázolni, csak a végső függvényt, akkor kiválaszod az alapfüggvény egy nevezetes pontját (az exponenciális függvények esetében ez mindig a (0;1) pont) és ezeken végzed el a transzformációkat.
Ábrán a lépések
II. `log_5 (x+2)-4`
1. `log_5 x` alapfüggvény
2. `log_5 (x+2)` eltolás az x tengely mentén negatív irányba 2 egységgel
3. `log_5 (x+2) -4` eltolás az y tengely mentén negatív irányba 4 egységgel.
A logaritmus függvény 1-nél nagyobb alap esetén növekvő, 0-1 közötti esetben csökkenő (szig. mon.). Fix pontnak érdemes kiválasztani az (1;0) pontot.
Ábra.
III. `(1/3)^(x+2)+3`
Az egynél kisebb alap (`1/3`) miatt az alapfüggvény szigorúan monoton csökkenő.
1. `y=(1/3)^x` alapfüggvény
2. `y=(1/3)^(x+2)` eltolás az x tengely mentén negatív irányba 2 egységgel
3. `y=(1/3)^(x+2)+3` eltolás az y tengely mentén pozitív irányba 3 egységgel.
Itt is a (0;1) pontot érdemes eltolni, így a függény képe olyan lesz, mint az alapfüggvényé, csak (-2;3) vektorral eltolva.
Ábra
1. Először ábrázolod az alapfüggvényt, az `4^x` lesz. Az exponenciális függvényeknek két alapesete van, ha az alap egynél nagyobb, akkor szigorúan monoton növekvő, ha egynél kisebb (0 és 1 közötti), akkor szigorúan monoton csökkenő.
A függvényábrázolások alapesetei:
- A függvény argumentumában végezzük el a műveletet (x helyett x-1 lesz a kitevőben). Ilyenkor az x tengely mentén történik az eltolás, ellentétes előjellel, mint a feltüntetett művelet. A mi konkrét példánkban itt eltolás történik 1 egységgel pozitív irányba.
- A függvény argumentumán kívül történik a transzformáció, (itt kivonunk kettőt az exponenciális kifejezésből). Ekkor eltolás történik, csak az y tengely mentén, megegyező előjellel. A konkrét példában 2 egységgel negatív irányba.
- Lehet még tükrözés abban az esetben, ha szorzunk -1-gyel, vagy eléteszünk egy mínusz jelet. (ha lesz ilyen, majd mutatom)
- Nyújtás, zsugorítás. A függvényt szorozzuk, osztjuk valamilyen valós számmal. (később, ha lesz ilyen)
Ha nem akarod mindegyik függvényt ábrázolni, csak a végső függvényt, akkor kiválaszod az alapfüggvény egy nevezetes pontját (az exponenciális függvények esetében ez mindig a (0;1) pont) és ezeken végzed el a transzformációkat.
Ábrán a lépések
II. `log_5 (x+2)-4`
1. `log_5 x` alapfüggvény
2. `log_5 (x+2)` eltolás az x tengely mentén negatív irányba 2 egységgel
3. `log_5 (x+2) -4` eltolás az y tengely mentén negatív irányba 4 egységgel.
A logaritmus függvény 1-nél nagyobb alap esetén növekvő, 0-1 közötti esetben csökkenő (szig. mon.). Fix pontnak érdemes kiválasztani az (1;0) pontot.
Ábra.
III. `(1/3)^(x+2)+3`
Az egynél kisebb alap (`1/3`) miatt az alapfüggvény szigorúan monoton csökkenő.
1. `y=(1/3)^x` alapfüggvény
2. `y=(1/3)^(x+2)` eltolás az x tengely mentén negatív irányba 2 egységgel
3. `y=(1/3)^(x+2)+3` eltolás az y tengely mentén pozitív irányba 3 egységgel.
Itt is a (0;1) pontot érdemes eltolni, így a függény képe olyan lesz, mint az alapfüggvényé, csak (-2;3) vektorral eltolva.
Ábra
0
-
Fruzsiiiiiiiiiiiiiii: Köszönöm szépenn! 2 éve 0