Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Csempézéssel kapcsolatos geometriai feladvány és kérdés
 gyula205
kérdése
gyula205
kérdése
265
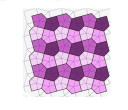
A mellékelt ábrán a sík csempézését (tessalációját) bemutató egybevágó nem
szabályos ötszögeket láthatunk. Ezzel kapcsolatban egy feladatot
és egy kérdést fogalmaztunk meg.
Látható, hogy az ötszöget két egybevágó négyszög és három
egybevágó deltoid alkotja. A feladat a következő: Ha feltételezzük, hogy
a négyszög oldala `sqrt(3)`, akkor mennyi az ötszög kerülete, területe
és a beírható kör sugara?
A kérdés pedig az, hogy ennek az ötszögnek létezik-e a körülírt
(a csúcspontokra illeszkedő) köre? Ha létezik, akkor mennyi a sugara?
Válaszokat megköszönnénk.
szabályos ötszögeket láthatunk. Ezzel kapcsolatban egy feladatot
és egy kérdést fogalmaztunk meg.
Látható, hogy az ötszöget két egybevágó négyszög és három
egybevágó deltoid alkotja. A feladat a következő: Ha feltételezzük, hogy
a négyszög oldala `sqrt(3)`, akkor mennyi az ötszög kerülete, területe
és a beírható kör sugara?
A kérdés pedig az, hogy ennek az ötszögnek létezik-e a körülírt
(a csúcspontokra illeszkedő) köre? Ha létezik, akkor mennyi a sugara?
Válaszokat megköszönnénk.
Jelenleg 1 felhasználó nézi ezt a kérdést.
Sokszögek, Tessaláció, Körülírt_kör
Sokszögek, Tessaláció, Körülírt_kör
0
Középiskola / Matematika
Válaszok
1 csettlik
válasza
csettlik
válasza
Az ötszög területe:
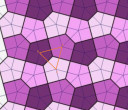
Az ábrán bejelölt narancs háromszög egy egyenlő oldalú háromszög (az ötszög oldalára merőleges a háromszög oldala mindkét térfélről, így biztos egy egyenesbe esik). Mindegyik oldala `2*sqrt(3)` egység hosszú. Az egyenlő oldalú háromszögről tudjuk, hogy minden nevezetes vonala egybeesik. Így a deltoid főátlóját kitudjuk számolni.
Vesszük a háromszög magasságát, amit Pitagorasz tétellel számolunk ki.
`m_"háromszög"=sqrt((2*sqrt(3))^2-(sqrt(3))^2)` ⇒ `m_"háromszög"=sqrt(4*3-3)` ⇒ `m_"háromszög"=3` egység.
A háromszöget három deltoid alkotja. A pont, ahol a három deltoid csúcsa találkozik egyben a háromszög súlypontja, amiről tudjuk, hogy a súlyvonalat kettő az egy arányba osztja. Így kapjuk meg a deltoid egyik átlójának a hosszát, ami `2` egység.
A deltoid rövidebb átlója a háromszög középvonalával esik egybe, amiről tudjuk a párhuzamos szelők tételéből, hogy fele az alap hosszának. A háromszög alapja `2*sqrt(3)`, így a középvonal `sqrt(3)` egység.
A deltoid területe: `T_"deltoid"=(e*f)/2`
`T_"deltoid"=(2*sqrt(3))/2=sqrt(3)` egység².
A négyzet területe: `T_"négyzet"=sqrt(3)^2=3` egység².
Az ötszög területe:
`T_"ötszög"=2*T_"négyzet"+3*T_"deltoid"=2*3+3*sqrt(3)=3*(2+sqrt(3))` egység²
Az ötszög kerülete:
Az ötszög kerülete áll négy darab négyzet oldalból és hat darab deltoid rövidebb oldalból. A négyzet oldalát ismerjük. A deltoid rövidebb oldalát kell kiszámolni:
A deltoid hosszabb átlója felezi a rövidebbet. Pitagorasz tétellel meghatározom a hosszabb oldal osztópontját, amiből aztán a rövidebb oldal kiszámolható.
`sqrt(3)^2=(sqrt(3)/2)^2+x^2`
`3=3/4+x^2`
`x=sqrt(9/4)=3/2` egység. Ez a hosszabb átló hosszabb fele. Így a rövidebb fél `2-3/2=1/2`
Innen jön a deltoid rövidebb oldala:
`y^2=(sqrt(3)/2)^2+(1/2)^2`
`y^2=3/4+1/4`
`y^2=1` ⇒ `y=1`
`K_"ötszög"=4*sqrt(3)+6*1=~12,93` egység.
A beírható kör sugara:
A beírható kör érintési pontjai és az oldal derékszöget zárnak be. Így az ábráról leolvasható, hogy `r=sqrt(3)`. A külső pontból húzott érintők azonos hosszúságúak az érintési pontig. A beírható kör középpontja a betűvel jelölt pontok egyike.
Sajnos a kérdésre, hogy létezik-e az ötszög köré írható kör, és annak mennyi a sugara, meghaladja a tudásomat. Arra gondoltam, hogy a beírható kör középpontja egybe esik a köré írható kör középpontjával, de az látható, hogy a négyzet átlója (`sqrt(6)`, míg a deltoid hosszabb átlója `2`. Így ezt a gondolatot el kellett vetni.
A próbálkozásaim nem vezettek eredményre, így azt gondolom, hogy nincs köré írható kör. De bizonyítani nem tudom. Kevés vagyok ehhez a feladathoz.
Kevés vagyok ehhez a feladathoz.
Az ábrán bejelölt narancs háromszög egy egyenlő oldalú háromszög (az ötszög oldalára merőleges a háromszög oldala mindkét térfélről, így biztos egy egyenesbe esik). Mindegyik oldala `2*sqrt(3)` egység hosszú. Az egyenlő oldalú háromszögről tudjuk, hogy minden nevezetes vonala egybeesik. Így a deltoid főátlóját kitudjuk számolni.
Vesszük a háromszög magasságát, amit Pitagorasz tétellel számolunk ki.
`m_"háromszög"=sqrt((2*sqrt(3))^2-(sqrt(3))^2)` ⇒ `m_"háromszög"=sqrt(4*3-3)` ⇒ `m_"háromszög"=3` egység.
A háromszöget három deltoid alkotja. A pont, ahol a három deltoid csúcsa találkozik egyben a háromszög súlypontja, amiről tudjuk, hogy a súlyvonalat kettő az egy arányba osztja. Így kapjuk meg a deltoid egyik átlójának a hosszát, ami `2` egység.
A deltoid rövidebb átlója a háromszög középvonalával esik egybe, amiről tudjuk a párhuzamos szelők tételéből, hogy fele az alap hosszának. A háromszög alapja `2*sqrt(3)`, így a középvonal `sqrt(3)` egység.
A deltoid területe: `T_"deltoid"=(e*f)/2`
`T_"deltoid"=(2*sqrt(3))/2=sqrt(3)` egység².
A négyzet területe: `T_"négyzet"=sqrt(3)^2=3` egység².
Az ötszög területe:
`T_"ötszög"=2*T_"négyzet"+3*T_"deltoid"=2*3+3*sqrt(3)=3*(2+sqrt(3))` egység²
Az ötszög kerülete:
Az ötszög kerülete áll négy darab négyzet oldalból és hat darab deltoid rövidebb oldalból. A négyzet oldalát ismerjük. A deltoid rövidebb oldalát kell kiszámolni:
A deltoid hosszabb átlója felezi a rövidebbet. Pitagorasz tétellel meghatározom a hosszabb oldal osztópontját, amiből aztán a rövidebb oldal kiszámolható.
`sqrt(3)^2=(sqrt(3)/2)^2+x^2`
`3=3/4+x^2`
`x=sqrt(9/4)=3/2` egység. Ez a hosszabb átló hosszabb fele. Így a rövidebb fél `2-3/2=1/2`
Innen jön a deltoid rövidebb oldala:
`y^2=(sqrt(3)/2)^2+(1/2)^2`
`y^2=3/4+1/4`
`y^2=1` ⇒ `y=1`
`K_"ötszög"=4*sqrt(3)+6*1=~12,93` egység.
A beírható kör sugara:
A beírható kör érintési pontjai és az oldal derékszöget zárnak be. Így az ábráról leolvasható, hogy `r=sqrt(3)`. A külső pontból húzott érintők azonos hosszúságúak az érintési pontig. A beírható kör középpontja a betűvel jelölt pontok egyike.
Sajnos a kérdésre, hogy létezik-e az ötszög köré írható kör, és annak mennyi a sugara, meghaladja a tudásomat. Arra gondoltam, hogy a beírható kör középpontja egybe esik a köré írható kör középpontjával, de az látható, hogy a négyzet átlója (`sqrt(6)`, míg a deltoid hosszabb átlója `2`. Így ezt a gondolatot el kellett vetni.
A próbálkozásaim nem vezettek eredményre, így azt gondolom, hogy nincs köré írható kör. De bizonyítani nem tudom.
 Kevés vagyok ehhez a feladathoz.
Kevés vagyok ehhez a feladathoz.
0
- Még nem érkezett komment!