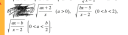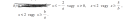Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Gyökös kifejezések értelmezési tartománya
 nemeth.istvan.alex
kérdése
nemeth.istvan.alex
kérdése
360
Jó napot! Valaki segítene az alábbi gyökös feladatok értelmezési tartományának meghatározásában? Megcsináltam a számításokat csak nem tudom leszűrni hogy végülis mi alapján az a megoldás ami.
Csatoltam a feladatot, megoldókulcsot és azt amit én csináltam.
Válaszokat előre is köszönöm!
Csatoltam a feladatot, megoldókulcsot és azt amit én csináltam.
Válaszokat előre is köszönöm!
Jelenleg 1 felhasználó nézi ezt a kérdést.
Gyökvonás, TÖRTEK
Gyökvonás, TÖRTEK
0
Középiskola / Matematika
Válaszok
1 kazah
megoldása
kazah
megoldása
`root()((ax+2)/x)`
Először vizsgálod, hogy a nevező nem lehet nulla, tehát `x ne 0`
Aztán a gyökjel alatti kifejezés nem lehet negatív
`(ax+2)/x` = `x*(a+2/x)/x` = `a+2/x`
x-szel egyszerűsíthettünk, mert nem nulla. Ez a kifejezés legyen nemnegatív.
`a+2/x ge 0` /-a
`2/x ge -a` /:2
`1/x ge -a/2` reciprok, a relációs jel megfordul
`x le -2/a`
Mivel a mindig pozitív, ezért lett odaírva a nagyobb, mint nulla.
`root()((bx-5)/(x-2))`
A nevező miatt `x ne 2`.
Lehet úgy is, (gondolom úgy tanítják) hogy egy tört akkor nemnegatív, ha
I. számláló és nevező is nemnegatív (a nevezőre a nulla is kikötés, tehát itt most pozitív)
II. a számláló és a nevező is nempozitív (a nevező negatív).
I.
`bx-5 ge 0 cap x gt 2`
`bx ge 5 cap x gt 2`
`x ge 5/b cap x gt 2`
Mivel b értéke 0 és 2 között van, így a megoldás: `x ge 5/b`
II.
`bx-5 le 0 cap x lt 2`
`bx le 5 cap x lt 2`
`x le 5/b cap x lt 2` `rightarrow` `x lt 2`
`root()((ax-b)/(x-2))`
Nevező nem nulla: `x ne 2`
I. számláló nemnegatív, nevező pozitív:
`ax-b ge 0 cap x gt 2`
`ax ge b cap x gt 2`
I. a Ha a pozitív, akkor
`x ge b/a cap x gt 2`
A `b/a` kifejezés értéke a megadott feltételek miatt mindig nagyobb +2-nél.
Megoldás: `x ge b/a`
I. b. Ha 'a' negatív:
`x le b/a cup x gt 2` `rightarrow` Nincs ilyen szám.
II. Ha a számláló és a nevező is negatív:
`ax-b lt 0 cap x le 2`
`ax lt b cap x le 2`
II. a. Ha 'a' pozitív:
`x gt b/a cap x le 2` Nincs ilyen szám.
II. b. Ha 'a' negatív:
`x lt b/a cap x le 2` `rightarrow` `x le 2`
Jók a levezetések, meg kell nézni a két feltétel metszetét és azzal megkapod a megoldásokat.
Először vizsgálod, hogy a nevező nem lehet nulla, tehát `x ne 0`
Aztán a gyökjel alatti kifejezés nem lehet negatív
`(ax+2)/x` = `x*(a+2/x)/x` = `a+2/x`
x-szel egyszerűsíthettünk, mert nem nulla. Ez a kifejezés legyen nemnegatív.
`a+2/x ge 0` /-a
`2/x ge -a` /:2
`1/x ge -a/2` reciprok, a relációs jel megfordul
`x le -2/a`
Mivel a mindig pozitív, ezért lett odaírva a nagyobb, mint nulla.
`root()((bx-5)/(x-2))`
A nevező miatt `x ne 2`.
Lehet úgy is, (gondolom úgy tanítják) hogy egy tört akkor nemnegatív, ha
I. számláló és nevező is nemnegatív (a nevezőre a nulla is kikötés, tehát itt most pozitív)
II. a számláló és a nevező is nempozitív (a nevező negatív).
I.
`bx-5 ge 0 cap x gt 2`
`bx ge 5 cap x gt 2`
`x ge 5/b cap x gt 2`
Mivel b értéke 0 és 2 között van, így a megoldás: `x ge 5/b`
II.
`bx-5 le 0 cap x lt 2`
`bx le 5 cap x lt 2`
`x le 5/b cap x lt 2` `rightarrow` `x lt 2`
`root()((ax-b)/(x-2))`
Nevező nem nulla: `x ne 2`
I. számláló nemnegatív, nevező pozitív:
`ax-b ge 0 cap x gt 2`
`ax ge b cap x gt 2`
I. a Ha a pozitív, akkor
`x ge b/a cap x gt 2`
A `b/a` kifejezés értéke a megadott feltételek miatt mindig nagyobb +2-nél.
Megoldás: `x ge b/a`
I. b. Ha 'a' negatív:
`x le b/a cup x gt 2` `rightarrow` Nincs ilyen szám.
II. Ha a számláló és a nevező is negatív:
`ax-b lt 0 cap x le 2`
`ax lt b cap x le 2`
II. a. Ha 'a' pozitív:
`x gt b/a cap x le 2` Nincs ilyen szám.
II. b. Ha 'a' negatív:
`x lt b/a cap x le 2` `rightarrow` `x le 2`
Jók a levezetések, meg kell nézni a két feltétel metszetét és azzal megkapod a megoldásokat.
1
-
nemeth.istvan.alex: Köszönöm szépen a segítséget! 2 éve 0