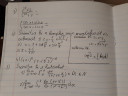Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Üdv! Pár matek analízis (gyakorlati) feladat. Légyszives segítsetek.. fontos lenne nekem.(+pontok ZH hoz)
 audiquattrolove
kérdése
audiquattrolove
kérdése
766
Csatoltam képet.
Jelenleg 1 felhasználó nézi ezt a kérdést.
matekanalizis
matekanalizis
0
Felsőoktatás / Matematika
Válaszok
3 bongolo
{
bongolo
{  }
válasza
}
válasza
1)
`i^5=i·(i^2)^2=i`
`i^(19)=i·(i^2)^9=-i`
`(i^5+2)/(i^(19)+1)=(2+i)/(1-i)`
Bővítsük `(1+i)`-vel:
`=((2+i)(1+i)/(1^2-i^2)=(2+3i-1)/(2)=(1+3i)/2`
`(cosx+sinx)/(cosx-sinx)`
Bővítsük `(cosx+sinx)`-szel:
`=(cosx+sinx)^2/(cos^2x-sin^2x)=(sin^2x+2·sinx·cosx+cos^2x)/(cos2x)=(1+sin2x)/(cos2x)`
`i^5=i·(i^2)^2=i`
`i^(19)=i·(i^2)^9=-i`
`(i^5+2)/(i^(19)+1)=(2+i)/(1-i)`
Bővítsük `(1+i)`-vel:
`=((2+i)(1+i)/(1^2-i^2)=(2+3i-1)/(2)=(1+3i)/2`
`(cosx+sinx)/(cosx-sinx)`
Bővítsük `(cosx+sinx)`-szel:
`=(cosx+sinx)^2/(cos^2x-sin^2x)=(sin^2x+2·sinx·cosx+cos^2x)/(cos2x)=(1+sin2x)/(cos2x)`
1
- Még nem érkezett komment!
 bongolo
{
bongolo
{  }
válasza
}
válasza
2)
A modulus tényleg az, vagyis a komplex szám "vektorának" a hossza. (Persze az nem vektor!) Kicsit elírtad azért a modulus képlete előtt a `z`-t, hiányzik belőle az i:
`z=x+y·i`
`|z|=sqrt(x^2+y^2)`
Az argumentum (vagy arkusz) a "vektor" szöge:
`"arg"\ z = φ = "arc tg"\ |y/x|` ilyesmi, csak kicsit variálni kell a síknegyeddel, hogy 0-tól 360°-ig jöjjön ki a `φ`.
a) `z=-1/2+sqrt3/2i`
`|z|=sqrt(1/4+3/4)=1`
`φ="arc tg"sqrt3=π/3`
de `z` a II. síknegyedben van (mert a valós rész negatív, a képzetes pozitív), ezért
`"arg"\ z = π-φ=(2π)/3`
b) Itt valamit elírtál... lehet, hogy így lenne igaziból:
`z=1·("cos"π/7+i·"sin"π/7")`
Erről minden számolás nélkül leolvasható, hogy `|z|=1` és `"arg"\ z=π/7`
c)
`z=(1-i)/(1+i)`
A nevezőt valóssá lehet alakítani, ha bővítjük a törtet a nevező konjugáltjával (vagyis (1-i)-vel... ami teljesen véletlenül most ugyanannyi, mint a számláló, de az ne zavarjon meg):
`z=(1-i)^2/(1-i^2)=(1-2i+i^2)/(1-(-1)) = (1-2i-1)/2=-i`
Ezt fejből is lehet (kell) tudni, hogy `|z|=1` és `"arg"\ z=(3π)/2`
d)
Ha hatványozni kell, azt már nagyon nem érdemes algebrai alakban csinálni, inkább a modulusokkal és az argumentumokkal jobb dolgozni:
`z_1=1+i`
`|z_1|=sqrt(1+1)=sqrt2`
`φ_1="arc tg"\ 1/1=π/4`
Ez egyben az argumentum is, mert az első síknegyedben van `z_1`.
Ennek a 8-adik hatványa:
`|z_1^8|=|z_1|^8=sqrt2^8=2^4=16`
`"arg"(z_1^8)=8·"arg"\ z_1=2π` ami ugyanaz, mint a 0.
`z_2=1-i·sqrt3`
`|z_2|=sqrt(1+3)=2`
`φ_2="arc tg"\ sqrt3/1=π/3`
Mivel `z_2` a negyedik síknegyedben van (az imaginárius negatív), az argumentum:
`"arg"\ z_2=2π-φ_2=(5π)/3`
Ennek a -6-odik hatványa:
`|z_2^(-6)|=|z_2|^(-6)=1/sqrt2^6=1/2^3=1/8`
`"arg"(z_2^(-6))=-6·"arg"\ z_2=-10π=-5·2π` vagyis ez is ugyanaz, mint a 0.
Ennek a kettőnek a szorzata kell:
`|z|=|z_1^8|·|z_2^(-6)|=16·1/8=2`
`"arg"\ z="arg"(z_1^8)+"arg"(z_2^(-6))=0`
Vagyis `z=2`.
A modulus tényleg az, vagyis a komplex szám "vektorának" a hossza. (Persze az nem vektor!) Kicsit elírtad azért a modulus képlete előtt a `z`-t, hiányzik belőle az i:
`z=x+y·i`
`|z|=sqrt(x^2+y^2)`
Az argumentum (vagy arkusz) a "vektor" szöge:
`"arg"\ z = φ = "arc tg"\ |y/x|` ilyesmi, csak kicsit variálni kell a síknegyeddel, hogy 0-tól 360°-ig jöjjön ki a `φ`.
a) `z=-1/2+sqrt3/2i`
`|z|=sqrt(1/4+3/4)=1`
`φ="arc tg"sqrt3=π/3`
de `z` a II. síknegyedben van (mert a valós rész negatív, a képzetes pozitív), ezért
`"arg"\ z = π-φ=(2π)/3`
b) Itt valamit elírtál... lehet, hogy így lenne igaziból:
`z=1·("cos"π/7+i·"sin"π/7")`
Erről minden számolás nélkül leolvasható, hogy `|z|=1` és `"arg"\ z=π/7`
c)
`z=(1-i)/(1+i)`
A nevezőt valóssá lehet alakítani, ha bővítjük a törtet a nevező konjugáltjával (vagyis (1-i)-vel... ami teljesen véletlenül most ugyanannyi, mint a számláló, de az ne zavarjon meg):
`z=(1-i)^2/(1-i^2)=(1-2i+i^2)/(1-(-1)) = (1-2i-1)/2=-i`
Ezt fejből is lehet (kell) tudni, hogy `|z|=1` és `"arg"\ z=(3π)/2`
d)
Ha hatványozni kell, azt már nagyon nem érdemes algebrai alakban csinálni, inkább a modulusokkal és az argumentumokkal jobb dolgozni:
`z_1=1+i`
`|z_1|=sqrt(1+1)=sqrt2`
`φ_1="arc tg"\ 1/1=π/4`
Ez egyben az argumentum is, mert az első síknegyedben van `z_1`.
Ennek a 8-adik hatványa:
`|z_1^8|=|z_1|^8=sqrt2^8=2^4=16`
`"arg"(z_1^8)=8·"arg"\ z_1=2π` ami ugyanaz, mint a 0.
`z_2=1-i·sqrt3`
`|z_2|=sqrt(1+3)=2`
`φ_2="arc tg"\ sqrt3/1=π/3`
Mivel `z_2` a negyedik síknegyedben van (az imaginárius negatív), az argumentum:
`"arg"\ z_2=2π-φ_2=(5π)/3`
Ennek a -6-odik hatványa:
`|z_2^(-6)|=|z_2|^(-6)=1/sqrt2^6=1/2^3=1/8`
`"arg"(z_2^(-6))=-6·"arg"\ z_2=-10π=-5·2π` vagyis ez is ugyanaz, mint a 0.
Ennek a kettőnek a szorzata kell:
`|z|=|z_1^8|·|z_2^(-6)|=16·1/8=2`
`"arg"\ z="arg"(z_1^8)+"arg"(z_2^(-6))=0`
Vagyis `z=2`.
1
- Még nem érkezett komment!
 bongolo
{
bongolo
{  }
megoldása
}
megoldása
3)
Az elsőt nem tudom elolvasni. Ilyennek látszik:
`lim_(n->∞)int_0^1 (dx)/(1+(1+x/n)n)`
de mi az az "`i n ∈ ℕ`", vagy valahol máshol van az `i`?
Ha így van:
`=lim_(n->∞) int_0^1(dx)/(1+n+x)`
ahol
`1/(n+(x+1)) < 1/n`, hisz `x >= 0`, tehát az integrál felső közelítő összege lehet egy `1/n` magas és 1 széles téglalap, aminek a területe `1/n`. Így a határérték ez:
`=lim_(n->∞) 1/n = 0`
A másodiknál:
Alfa akar lenni az az írott nagy L-betűnek kinéző dolog?
`lim_(α->∞) int_1^2 ("ln"(x+|α|))/("ln"(x^2+α^2)) dx`
(az abszolút értéknek nincs sok jelentősége, hisz α a plusz végtelenhez tart, pozitív)
A limeszt be lehet vinni az integrál belsejébe. Nézzük így az integrál belsejét (lehagytam az abszolút érték jelet, de ha kiírod, az se tesz semmi változást):
`lim_(α->∞)("ln"(x+α))/("ln"(x^2+α^2))`
`=lim_(α->∞)("ln"(x/α+1)+"ln"\ α)/("ln"((x/α)^2+1)+"ln"\ α^2)`
`x/α` határértéke 0, azok helyett be lehet írni a nullát. És persze `"ln"\ 1 = 0`, tehát ez lett a limesz:
`=lim_(α->∞)("ln"\ α)/("ln"\ α^2)=lim_(α->∞)("ln"\ α)/(2·"ln"\ α)=1/2`
Az integrál pedig:
`int_1^2 1/2 dx = 1/2·(2-1) = 1/2`
Az elsőt nem tudom elolvasni. Ilyennek látszik:
`lim_(n->∞)int_0^1 (dx)/(1+(1+x/n)n)`
de mi az az "`i n ∈ ℕ`", vagy valahol máshol van az `i`?
Ha így van:
`=lim_(n->∞) int_0^1(dx)/(1+n+x)`
ahol
`1/(n+(x+1)) < 1/n`, hisz `x >= 0`, tehát az integrál felső közelítő összege lehet egy `1/n` magas és 1 széles téglalap, aminek a területe `1/n`. Így a határérték ez:
`=lim_(n->∞) 1/n = 0`
A másodiknál:
Alfa akar lenni az az írott nagy L-betűnek kinéző dolog?
`lim_(α->∞) int_1^2 ("ln"(x+|α|))/("ln"(x^2+α^2)) dx`
(az abszolút értéknek nincs sok jelentősége, hisz α a plusz végtelenhez tart, pozitív)
A limeszt be lehet vinni az integrál belsejébe. Nézzük így az integrál belsejét (lehagytam az abszolút érték jelet, de ha kiírod, az se tesz semmi változást):
`lim_(α->∞)("ln"(x+α))/("ln"(x^2+α^2))`
`=lim_(α->∞)("ln"(x/α+1)+"ln"\ α)/("ln"((x/α)^2+1)+"ln"\ α^2)`
`x/α` határértéke 0, azok helyett be lehet írni a nullát. És persze `"ln"\ 1 = 0`, tehát ez lett a limesz:
`=lim_(α->∞)("ln"\ α)/("ln"\ α^2)=lim_(α->∞)("ln"\ α)/(2·"ln"\ α)=1/2`
Az integrál pedig:
`int_1^2 1/2 dx = 1/2·(2-1) = 1/2`
1
-
audiquattrolove: Köszönöm szépen , hogy segített és foglalkozott vele ! Ön igazán Okos ember !
 8 éve
0
8 éve
0