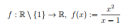Toplista
- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
A képen szereplő függvény vizsgálata az alábbi szempontok szerint
gyusszancs
kérdése
519
határértékek ±∞-ben és a szakadási pontban, monotonitás, lokális szélsőértékek, konvexitás, inflexiós pontok
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Felsőoktatás / Matematika
Válaszok
2
AlBundy
{ Polihisztor }
megoldása
A számláló gyorsabban tart `oo`-hez, mint a nevező, ezért a határérték nem véges:
`lim_(x->oo) x^2/(x-1)=oo`
`lim_(x->-oo) x^2/(x-1)=-oo`
A szakadási pontban nem létezik a határérték, mivel a szakadás másodfajú, és a bal oldali határérték `-oo`, a jobb oldali pedig `oo` (lásd a mellékelt grafikont).
A függvény deriváltja: `(2x*(x-1)-x^2*1)/(x-1)^2=(x^2-2x)/(x-1)^2=(x(x-2))/(x-1)^2`
A nevező sosem negatív. A számláló pozitív, ha `x>2` vagy ha `x < 0`. Ezeken a szakaszokon tehát a függvény monoton növekvő. A `0 < x < 2` intervallumon a derivált negatív, ekkor monoton csökkenő (kivéve a szakadási pontot). A derivált nulla az `x=0` és `x=2` helyeken, itt lokális szélsőértékek vannak.
A második derivált:
`d/dx[(x^2-2x)/(x^2-2x+1)]``=``((2x-2)*(x^2-2x+1)-(x^2-2x)*(2x-2))/((x-1)^4)``=``(2x-2)/(x-1)^4``=``2/(x-1)^3`
Ez negatív, ha `x < 1` (itt a függvény konkáv) és pozitív, ha `x > 1` (itt pedig konvex). Vagyis az `x=0` helyen lévő lokális szélsőérték egy lokális maximum, az `x=2` helyen lévő pedig lokális minimum. A második derivált sosem nulla, tehát inflexiós pont nincs.
`lim_(x->oo) x^2/(x-1)=oo`
`lim_(x->-oo) x^2/(x-1)=-oo`
A szakadási pontban nem létezik a határérték, mivel a szakadás másodfajú, és a bal oldali határérték `-oo`, a jobb oldali pedig `oo` (lásd a mellékelt grafikont).
A függvény deriváltja: `(2x*(x-1)-x^2*1)/(x-1)^2=(x^2-2x)/(x-1)^2=(x(x-2))/(x-1)^2`
A nevező sosem negatív. A számláló pozitív, ha `x>2` vagy ha `x < 0`. Ezeken a szakaszokon tehát a függvény monoton növekvő. A `0 < x < 2` intervallumon a derivált negatív, ekkor monoton csökkenő (kivéve a szakadási pontot). A derivált nulla az `x=0` és `x=2` helyeken, itt lokális szélsőértékek vannak.
A második derivált:
`d/dx[(x^2-2x)/(x^2-2x+1)]``=``((2x-2)*(x^2-2x+1)-(x^2-2x)*(2x-2))/((x-1)^4)``=``(2x-2)/(x-1)^4``=``2/(x-1)^3`
Ez negatív, ha `x < 1` (itt a függvény konkáv) és pozitív, ha `x > 1` (itt pedig konvex). Vagyis az `x=0` helyen lévő lokális szélsőérték egy lokális maximum, az `x=2` helyen lévő pedig lokális minimum. A második derivált sosem nulla, tehát inflexiós pont nincs.
Módosítva: 7 éve
0
- Még nem érkezett komment!
