Geometria

Először egy tételre hívnám fe a figyelmet. Ha két háromszögnek egy oldala közös, s az egyik
háromszög a másikat tartalmazza, akkor a közös oldallal szemben a tartalmazó háromszögben
kisebb szög van, mint a tartalmazottban.

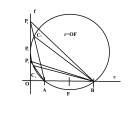
Vegyünk fel egy `e` egyenest és rajta két különböző pontot, `A`-t és `B`-t. (Lásd a csatolt ábrát is) Húzzunk egy `f` merőlegest az `e` egyenesre, amely nem metszi az `AB` szakaszt. Legyen a két egyenes metszéspontja az `O` pont és az `AB` szakasz felezője az `F` pontban. Szerkesszünk egy kört, amely átmegy a szakasz két `A` és `B` végpontján és érinti az `f ` egyenest. Legyen az érintési pont a `P_0` pontban. Az jól látható, hogy a kör középontja illeszkedik az `AB` szakaszfelező merőlegesére, és a kör sugara az `OF` távolság lesz. Állítátjuk, hogy így eljutunk feladat megoldásához is.

Az `f ` egyenes `P_0`-tól különböző pontjai mind a körön kivül vannak, tehát mindegyikükből kisebb szögben látszik, mint a `P_0`-ból.

Vegyünk fel tetszőlegesen egy `P_1` pontot az `OP_0` szakaszból. Kössük össze a `P_1` pontot az `A` és a `B` pontokkal. Ekkor `P_1A`-hoz tartozó egyenes `C_1` pontban metszi a kört és `BP_1A triangle` tartalmazza `BC_1A triangle`-et, ezért `BP_1A angle < BC_1A angle`.

Majd ismételten vegyünk fel tetszőlegesen egy `P_2` pontot az `O` pontot nem tartalmazó az az `f` egyenesre illeszkedő `P_0` ponttal kezdődő félegyenesen is. Itt is látható, hogy `P_2A`-hoz tartozó egyenes `C_2` pontban metszi a kört és `BP_2A triangle` tartalmazza `BC_2A triangle`-et, ezért `BP_2A angle < BC_2A angle` .

Az is jól látható, hogy `BC_1A angle`, `BP_0A angle`, `BC_2A angle` szögek ugyanahhoz a
körívhez tartozó kerületi szögek és azonosak egymással. Ezek mindegyike nagyobbak lesznek, mint az `f` egyenes azon pontjaihoz tartozó látószögek ahonnan az `AB` szakasz látszik. Így a feladat megoldását a `P_0` pont szolgáltatja.