Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Sziasztok! Ebben a matek feladatban tudna valaki segíteni? Előre is köszönöm.
 Dávid Klár
kérdése
Dávid Klár
kérdése
350
Adottak az:
e: 5x-2y=-7
g: C*X +4y =5 egyenesek
Milyen C valós szám esetén lesz az e egyenesre merőleges a g egyenes?
e: 5x-2y=-7
g: C*X +4y =5 egyenesek
Milyen C valós szám esetén lesz az e egyenesre merőleges a g egyenes?
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Középiskola / Matematika
Válaszok
1 meika
{ Vegyész }
válasza
meika
{ Vegyész }
válasza
Alakítsuk át:
e: 5x-2y=-7
-2y=-7-5x
y=2,5x+3,5
g: C*X +4y =5
4y =5-C*X
y=(-C/4)*X+1,25
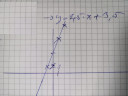
A rajz segít kicsit jobban átlátni.
Egy g egyenest keresünk, ami átmegy a (0;1,25) ponton és merőleges az e egyenesre.
Másképpen: ha felírjuk az e egyenes irány vektorát, akkor az a g egyenes normál vektora lesz.
az e egyenes irány vektora: (2;5) (egy origóból induló, e-vel párhuzamos vektor)
A g egyenes normál vektoros egyenlete:
n₁x+n₂y=n₁x₀+n₂y₂ (n₁;n₂) a normál vektor koordinátái, (x₀;y₀) a pont, amin átmegy, jelen esetben a (0;1,25) tengelymetszet.
g: 2x+5y=2*0 + 5*1,25
g: 2x+5y=6,25
g: 5y=-2x+6,25 ( :5 )
g: y=(-2/5)x+1,25
Tehát az X együtthatóival:
(-C/4) = (-2/5)
C=8/5 valós szám esetén lesz az e egyenesre merőleges a g egyenes.
És valóban, az y=-0,4*x+1,25 egyenes merőleges lesz az e-re.
e: 5x-2y=-7
-2y=-7-5x
y=2,5x+3,5
g: C*X +4y =5
4y =5-C*X
y=(-C/4)*X+1,25
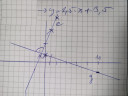
A rajz segít kicsit jobban átlátni.
Egy g egyenest keresünk, ami átmegy a (0;1,25) ponton és merőleges az e egyenesre.
Másképpen: ha felírjuk az e egyenes irány vektorát, akkor az a g egyenes normál vektora lesz.
az e egyenes irány vektora: (2;5) (egy origóból induló, e-vel párhuzamos vektor)
A g egyenes normál vektoros egyenlete:
n₁x+n₂y=n₁x₀+n₂y₂ (n₁;n₂) a normál vektor koordinátái, (x₀;y₀) a pont, amin átmegy, jelen esetben a (0;1,25) tengelymetszet.
g: 2x+5y=2*0 + 5*1,25
g: 2x+5y=6,25
g: 5y=-2x+6,25 ( :5 )
g: y=(-2/5)x+1,25
Tehát az X együtthatóival:
(-C/4) = (-2/5)
C=8/5 valós szám esetén lesz az e egyenesre merőleges a g egyenes.
És valóban, az y=-0,4*x+1,25 egyenes merőleges lesz az e-re.
0
- Még nem érkezett komment!