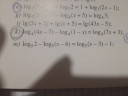Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Exp. egyenlet, logaritmus
 Boglárka
kérdése
Boglárka
kérdése
466
Ezeket meg tudná valaki oldani?
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Középiskola / Matematika
Válaszok
2 bongolo
{
bongolo
{  }
megoldása
}
megoldása
Az első egyenlet:
`5·3^(x+2)-7·2^(y-1)=17`
`5·3^2·3^(x)-7·2^(-1)·2^(y)=17`
`45·3^(x)-7/2·2^(y)=17`
A másik egyenlet:
`4·3^(x+1)-5·2^(y-3)=17`
`4·3·3^(x)-5·2^(-3)·2^(y)=17`
`12·3^(x)-5/8·2^(y)=17`
----
Vezessünk be két új ismeretlent:
`u=3^x`
`v=2^y`
A két egyenlet:
`45·u-7/2·v=17`
`12·u-5/8·v=17`
Oldd meg ezekből `u` és `v`-t, stb. Gondolom menni fog. Ha elakadsz, szólj.
`5·3^(x+2)-7·2^(y-1)=17`
`5·3^2·3^(x)-7·2^(-1)·2^(y)=17`
`45·3^(x)-7/2·2^(y)=17`
A másik egyenlet:
`4·3^(x+1)-5·2^(y-3)=17`
`4·3·3^(x)-5·2^(-3)·2^(y)=17`
`12·3^(x)-5/8·2^(y)=17`
----
Vezessünk be két új ismeretlent:
`u=3^x`
`v=2^y`
A két egyenlet:
`45·u-7/2·v=17`
`12·u-5/8·v=17`
Oldd meg ezekből `u` és `v`-t, stb. Gondolom menni fog. Ha elakadsz, szólj.
0
-
Boglárka: Igen menni 8 éve 0
 bongolo
{
bongolo
{  }
válasza
}
válasza
c)
Első egyenlet:
`(25^x)^y=125`
`25^(x·y)=125= 5^3`
`(5^2)^(x·y)=5^3`
`5^(2xy)=5^3`
ami azt jelenti, hogy `2xy=3`
Második egyenlet:
`4^(x·y)·2^x=2·8^(1/y)`
`(2^2)^(x·y)·2^x=2·(2^3)^(1/y)`
`2^(2xy)·2^x=2·2^(3/y)`
`2^(2xy+x)=2^(1+3/y)`
ami azt jelenti, hogy `2xy+x=1+3/y`
mindkét esetben az utolsó lépést azért lehetett megtenni, mert az exponenciális függvény szigorúan monoton.
Ez lett tehát:
`2xy=3`
`2xy+x=1+3/y`
Ez sima kétismeretlenes egyenletrendszer. Mondjuk az elsőből fejezd ki y-t `(y=3/(2x))` és írd be a másodikba:
`2x·3/(2x)+x=1+3/(3/(2x))`
Innen már gondolom be tudod fejezni...
Első egyenlet:
`(25^x)^y=125`
`25^(x·y)=125= 5^3`
`(5^2)^(x·y)=5^3`
`5^(2xy)=5^3`
ami azt jelenti, hogy `2xy=3`
Második egyenlet:
`4^(x·y)·2^x=2·8^(1/y)`
`(2^2)^(x·y)·2^x=2·(2^3)^(1/y)`
`2^(2xy)·2^x=2·2^(3/y)`
`2^(2xy+x)=2^(1+3/y)`
ami azt jelenti, hogy `2xy+x=1+3/y`
mindkét esetben az utolsó lépést azért lehetett megtenni, mert az exponenciális függvény szigorúan monoton.
Ez lett tehát:
`2xy=3`
`2xy+x=1+3/y`
Ez sima kétismeretlenes egyenletrendszer. Mondjuk az elsőből fejezd ki y-t `(y=3/(2x))` és írd be a másodikba:
`2x·3/(2x)+x=1+3/(3/(2x))`
Innen már gondolom be tudod fejezni...
0
- Még nem érkezett komment!