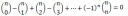Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Kombinatorika
 EzIsFoglaltNevci
kérdése
EzIsFoglaltNevci
kérdése
407
Igazoljuk az alábbi összefüggést!
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Felsőoktatás / Matematika
Válaszok
1 bongolo
{
bongolo
{  }
válasza
}
válasza
Ha n páratlan, vagyis `((n),(n))` negatív előjelű:
Tudjuk, hogy
`((n),(k)) = ((n),(n-k))`
Páratlan n esetén `((n),(0))` egyező értékű párja, vagyis `((n),(n))` kiejtik egymást, mert éppen ellentétes az előjelük. `((n),(1))`-hez tartozik `((n),(n-1))`, azok is kiejtik egymást, stb. Páratlan n esetén éppen páros darab tagból áll a váltott előjelű összeg, tehát mindegyiknek van ellentétes előjelű párja, 0 lesz az összeg.
Kombinatorikai igazolás arra az esetre, ha n páros:
Ekkor ezt kell igazolni:
`((n),(0))+((n),(2))+...+((n),(n)) = ((n),(1))+((n),(3))+...+((n),(n-1))`
A bal oldalon az van, hogy n elemből hányféleképpen választhatunk ki páros darabot, a jobb oldalon meg az, hogy páratlant.
Nézzünk kicsit mást: `n-1` elemű halmaznak `2^(n-1)` részhalmaza van, vagyis annyiféleképpen tudunk kiválasztani belőle bármit. A bármi az, hogy páros vagy páratlan darab elemet.
Vegyük most az `n` elemű halmazt. Az első `n-1` elemből csináljuk az előző "bármi" kiválasztást. Ha páros elem jött ki, adjuk hozzá a halmazhoz az `n`-edik elemet is, ha páratlan, akkor ne adjuk hozzá. Amit így kaptunk, az pont az, hogy a nagy halmazból kiválasztottunk páratlan darab elemet. Ez tehát a jobb oldal. Annak az összege tehát `2^(n-1)`.
Ha ehhez a páros elemű kiválasztásokat is hozzáadnánk, megkapnánk az összes lehetséges részhalmazt, ami `2^n`. Vagyis a párosak száma `2^n-2^(n-1)=2^(n-1)`, megegyezik a páratlanokkal.
Tudjuk, hogy
`((n),(k)) = ((n),(n-k))`
Páratlan n esetén `((n),(0))` egyező értékű párja, vagyis `((n),(n))` kiejtik egymást, mert éppen ellentétes az előjelük. `((n),(1))`-hez tartozik `((n),(n-1))`, azok is kiejtik egymást, stb. Páratlan n esetén éppen páros darab tagból áll a váltott előjelű összeg, tehát mindegyiknek van ellentétes előjelű párja, 0 lesz az összeg.
Kombinatorikai igazolás arra az esetre, ha n páros:
Ekkor ezt kell igazolni:
`((n),(0))+((n),(2))+...+((n),(n)) = ((n),(1))+((n),(3))+...+((n),(n-1))`
A bal oldalon az van, hogy n elemből hányféleképpen választhatunk ki páros darabot, a jobb oldalon meg az, hogy páratlant.
Nézzünk kicsit mást: `n-1` elemű halmaznak `2^(n-1)` részhalmaza van, vagyis annyiféleképpen tudunk kiválasztani belőle bármit. A bármi az, hogy páros vagy páratlan darab elemet.
Vegyük most az `n` elemű halmazt. Az első `n-1` elemből csináljuk az előző "bármi" kiválasztást. Ha páros elem jött ki, adjuk hozzá a halmazhoz az `n`-edik elemet is, ha páratlan, akkor ne adjuk hozzá. Amit így kaptunk, az pont az, hogy a nagy halmazból kiválasztottunk páratlan darab elemet. Ez tehát a jobb oldal. Annak az összege tehát `2^(n-1)`.
Ha ehhez a páros elemű kiválasztásokat is hozzáadnánk, megkapnánk az összes lehetséges részhalmazt, ami `2^n`. Vagyis a párosak száma `2^n-2^(n-1)=2^(n-1)`, megegyezik a páratlanokkal.
Módosítva: 8 éve
0
- Még nem érkezett komment!