Toplista
- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Sokszöges feladat
Törölt
kérdése
336
Egy 7 szög köré írható kör területe 267 cm². Számítsa ki a hétszög egy csúcsából húzható átlók hosszát. Továbbá számítsa ki az átlók által létrehozott háromszögek területét.
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Középiskola / Matematika
Válaszok
1
bazsa990608
{ Közgazdász }
megoldása
Köréírt kör sugara: `R=sqrt(T/pi)=sqrt(267/pi)=color(red)(9,22 \ cm)`
Sokszög oldalának hossza: `a=R*2sin \ (180°)/n=9,22*2sin \ (180°)/7=color(red)(8 \ cm)`
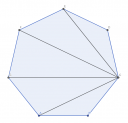
Az ábrán látható, hogy: `"AC"="EC"` valamint `"FC"="GC"`.
A hétszög egy belső szöge: `alpha=((n-2)*180°)/n=((7-2)*180°)/7=color(red)(128,57°)`
`"EC"=sqrt(2*8^2-2*8^2*cos128,57°)=color(red)(14,42 \ cm)`
Tehát `"AC"="EC"=14,42 \ cm`
`GhatAC=alpha-(180°-alpha)/2=128,57°-(180°-128,57°)/2=color(red)(102,855°)`
`"GC"=sqrt(8^2+14,92^2-2*8*14,92*cos102,855°)=color(red)(17,98 \ cm)`
`"FC"="GC"=17,98 \ cm`
`GhatAC=FhatEC=102,855°`
`T_(EDCtriangle)=T_(ABCtriangle)=(a^2*sinalpha)/2=(8^2*sin128,57°)/2=color(red)(25,02 \ cm^2)`
`T_(ECFtriangle)=T_(GCAtriangle)=(a*EC*sinFhatEC)/2=(8*14,42*sin102,855°)/2=color(red)(56,23 \ cm^2)`
`T_("hétszög")=(n*a^2*cot \ (180°)/n)/4=(7*8^2*cot \ (180°)/7)/4=color(red)(232,57 \ cm^2)`
`T_(FACtriangle)=T_("hétszög")-T_(EDCtriangle)-T_(ABCtriangle)-T_(ECFtriangle)-T_(GCAtriangle)=232,57-25,02-25,02-56,23-56,23=color(red)(70,07 \ cm^2)`
Sokszög oldalának hossza: `a=R*2sin \ (180°)/n=9,22*2sin \ (180°)/7=color(red)(8 \ cm)`
Az ábrán látható, hogy: `"AC"="EC"` valamint `"FC"="GC"`.
A hétszög egy belső szöge: `alpha=((n-2)*180°)/n=((7-2)*180°)/7=color(red)(128,57°)`
`"EC"=sqrt(2*8^2-2*8^2*cos128,57°)=color(red)(14,42 \ cm)`
Tehát `"AC"="EC"=14,42 \ cm`
`GhatAC=alpha-(180°-alpha)/2=128,57°-(180°-128,57°)/2=color(red)(102,855°)`
`"GC"=sqrt(8^2+14,92^2-2*8*14,92*cos102,855°)=color(red)(17,98 \ cm)`
`"FC"="GC"=17,98 \ cm`
`GhatAC=FhatEC=102,855°`
`T_(EDCtriangle)=T_(ABCtriangle)=(a^2*sinalpha)/2=(8^2*sin128,57°)/2=color(red)(25,02 \ cm^2)`
`T_(ECFtriangle)=T_(GCAtriangle)=(a*EC*sinFhatEC)/2=(8*14,42*sin102,855°)/2=color(red)(56,23 \ cm^2)`
`T_("hétszög")=(n*a^2*cot \ (180°)/n)/4=(7*8^2*cot \ (180°)/7)/4=color(red)(232,57 \ cm^2)`
`T_(FACtriangle)=T_("hétszög")-T_(EDCtriangle)-T_(ABCtriangle)-T_(ECFtriangle)-T_(GCAtriangle)=232,57-25,02-25,02-56,23-56,23=color(red)(70,07 \ cm^2)`
1
- Még nem érkezett komment!