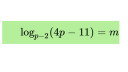Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Ebben a feladatban tudna esetleg valaki segíteni?
 Zsuzsanna255
kérdése
Zsuzsanna255
kérdése
358
Létezik-e olyan pozitív p prímszám, amelyre teljesül, hogy (csatolt kép) ha az m paraméter a 2023 valamelyik számjegye?
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Középiskola / Matematika
Válaszok
1 Ákos2
megoldása
Ákos2
megoldása
Logaritmus azonosság miatt kihozható hogy log_(p-2) (4p-11)= log(4p-11)/log(p-2)
Ezen a ponton ezt egyenlővé kell tenni a 2023 3db lehetséges számértékével(0,2,3)
m≠0, mivel a logaritmusok mindig 1nél nagyobb pozitiv számot adnak eredményül, így ez nem megoldás.
m=2=log(4p-11)/log(p-2) esetén átszorzunk
log(4p-11)=2*log(p-2).
ezután használunk egy újabb logaritmus azonosságot log(4p-11)=log(p-2)^2
Ezután a logarimtusoktól meg is szabadulhatunk 4p-11=(p-2)^2
4p-11= p^2-4p+4 innen a másodfokút rendezzük: p^2-8p+15=0
ezek megoldásai p=3 és p=5, amelyek mindketten prímszámok, de ha megnézzük az eredeti feladatot, log_(p-2)t adtak meg nekünk, és amennyiben p=3, akkor 1-es alapú logaritmusról beszélnénk, amely nem létezik (értelmetlen), így m=2 esetén p=5 megoldás
Hasonlóképp végigszámolható m=3 esetén is eljátszható ugyanez, ott is lesz egyszer eredmény a 3, mégegy tört szám amelyből ha kivonok 2-t nem több mint 1, tehát ismét nem megoldás, és 3,3028, amely megoldás de nem prím.
Ezen a ponton ezt egyenlővé kell tenni a 2023 3db lehetséges számértékével(0,2,3)
m≠0, mivel a logaritmusok mindig 1nél nagyobb pozitiv számot adnak eredményül, így ez nem megoldás.
m=2=log(4p-11)/log(p-2) esetén átszorzunk
log(4p-11)=2*log(p-2).
ezután használunk egy újabb logaritmus azonosságot log(4p-11)=log(p-2)^2
Ezután a logarimtusoktól meg is szabadulhatunk 4p-11=(p-2)^2
4p-11= p^2-4p+4 innen a másodfokút rendezzük: p^2-8p+15=0
ezek megoldásai p=3 és p=5, amelyek mindketten prímszámok, de ha megnézzük az eredeti feladatot, log_(p-2)t adtak meg nekünk, és amennyiben p=3, akkor 1-es alapú logaritmusról beszélnénk, amely nem létezik (értelmetlen), így m=2 esetén p=5 megoldás
Hasonlóképp végigszámolható m=3 esetén is eljátszható ugyanez, ott is lesz egyszer eredmény a 3, mégegy tört szám amelyből ha kivonok 2-t nem több mint 1, tehát ismét nem megoldás, és 3,3028, amely megoldás de nem prím.
Módosítva: 2 éve
1
- Még nem érkezett komment!