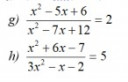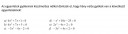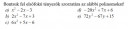Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Sok feladat
 kapocsaki
kérdése
kapocsaki
kérdése
371
Tudom, hogy sok feladat. Csak az csinálja meg aki élvezi és gyerekjáték neki, nem szeretnék sok időt rabolni.
Jelenleg 1 felhasználó nézi ezt a kérdést.
Matematika
Matematika
0
Középiskola / Matematika
Válaszok
6 RationalRick
{ Fizikus }
válasza
RationalRick
{ Fizikus }
válasza
Huh, ez sok lesz, de most nekiesek. Külön-külön válaszban fogom küldeni őket.
1. kép
`g)`
`(x^2-5x+6)/(x^2-7x+12)=2`
Itt érdemes átalakítani a gyöktényezős alakká:
`ax^2+bx+c=color(blue)(a(x-x_1)(x-x_2))`
Ehhez meg kell oldani a számlálót és a nevezőt is, mint másodfokút.
`x^2-5x+6=0`
`x_1=2`
`x_2=3`
A gyöktényezős alak: `(x-2)(x-3)`
`x^2-7x+12=0`
`x_1=3`
`x_2=4`
`(x-3)(x-4)`
Visszaírom:
`((x-2)(x-3))/((x-3)(x-4))=2`
`D=RR\\{3, 4}`, azaz az `x` nem lehet se három se négy, mert akkor nullával osztanánk
`((x-2)cancel((x-3)))/(cancel((x-3))(x-4))=2`
`(x-2)/(x-4)=2`
`x-2=2(x-4)`
`x-2=2x-8`
`x=6`
(A hat benne van az értelmezési tartományba, tehát jó lesz.)
`M={6}`
`h)`
`(x^2+6x-7)/(3x^2-x-2)=5`
`x^2+6x-7=0`
`x_1=-7`
`x_2=1`
`3x^2-x-2=0`
`x_1=-2/3`
`x_2=1`
`((x+7)(x-1))/(3(x+2/3)(x-1))=5`
`D=RR\\{-2/3; 1}`
`((x+7)cancel((x-1)))/(3(x+2/3)cancel((x-1)))=5`
`(x+7)/(3(x+2/3))=5`
`(x+7)/(3x+2)=5`
`x+7=5(3x+2)`
`x+7=15x+10`
`14x=-3`
`x=-3/14`
`x in D`
`M={-3/14}`
1. kép
`g)`
`(x^2-5x+6)/(x^2-7x+12)=2`
Itt érdemes átalakítani a gyöktényezős alakká:
`ax^2+bx+c=color(blue)(a(x-x_1)(x-x_2))`
Ehhez meg kell oldani a számlálót és a nevezőt is, mint másodfokút.
`x^2-5x+6=0`
`x_1=2`
`x_2=3`
A gyöktényezős alak: `(x-2)(x-3)`
`x^2-7x+12=0`
`x_1=3`
`x_2=4`
`(x-3)(x-4)`
Visszaírom:
`((x-2)(x-3))/((x-3)(x-4))=2`
`D=RR\\{3, 4}`, azaz az `x` nem lehet se három se négy, mert akkor nullával osztanánk
`((x-2)cancel((x-3)))/(cancel((x-3))(x-4))=2`
`(x-2)/(x-4)=2`
`x-2=2(x-4)`
`x-2=2x-8`
`x=6`
(A hat benne van az értelmezési tartományba, tehát jó lesz.)
`M={6}`
`h)`
`(x^2+6x-7)/(3x^2-x-2)=5`
`x^2+6x-7=0`
`x_1=-7`
`x_2=1`
`3x^2-x-2=0`
`x_1=-2/3`
`x_2=1`
`((x+7)(x-1))/(3(x+2/3)(x-1))=5`
`D=RR\\{-2/3; 1}`
`((x+7)cancel((x-1)))/(3(x+2/3)cancel((x-1)))=5`
`(x+7)/(3(x+2/3))=5`
`(x+7)/(3x+2)=5`
`x+7=5(3x+2)`
`x+7=15x+10`
`14x=-3`
`x=-3/14`
`x in D`
`M={-3/14}`
1
- Még nem érkezett komment!
 RationalRick
{ Fizikus }
válasza
RationalRick
{ Fizikus }
válasza
2. Viète-formulás kép:
Először is, a Viète-formulák:
`x_1+x_2=-b/a`
`x_1*x_2=c/a`
Itt már meg van adva két gyök már csak ki kell hozzá találni valamit. Pl.:
`a)`
`x_1=5`
`x_2=2`
`5+2=-b/a`
`7=-b/a`
Mondjuk akkor legyen a `b` 14, az `a` pedig `-2`
Kell még a c
`5*2=c/-2`
`c=-20`
És akkor az egyenlet:
`-2x^2+14-20=0`
Leegyszerűsítve:
`-x^2+7-10=0`
Mégegy:
`5*2=c/a`
Legyen a `c` 30 és az `a` 3.
Ekkor a `b`:
`7=-b/3`
`b=-21`
Az egyenlet:
`3x^2-21x+30=0`
`x^2-7x+10=0`
Láthatod, itt is szinte ugyanaz jött ki, csak -1-egy megszorozva, ami másodfokú esetén nem számít.
Tehát, akármit írsz eredetileg az `a`, `b`, `c` helyére, ha leegyszerűsíted a végén csak kettő marad (egymás ellentettei).
És ezt megcsinálhatod a többinél is, nekem már nincs rá időm.
Először is, a Viète-formulák:
`x_1+x_2=-b/a`
`x_1*x_2=c/a`
Itt már meg van adva két gyök már csak ki kell hozzá találni valamit. Pl.:
`a)`
`x_1=5`
`x_2=2`
`5+2=-b/a`
`7=-b/a`
Mondjuk akkor legyen a `b` 14, az `a` pedig `-2`
Kell még a c
`5*2=c/-2`
`c=-20`
És akkor az egyenlet:
`-2x^2+14-20=0`
Leegyszerűsítve:
`-x^2+7-10=0`
Mégegy:
`5*2=c/a`
Legyen a `c` 30 és az `a` 3.
Ekkor a `b`:
`7=-b/3`
`b=-21`
Az egyenlet:
`3x^2-21x+30=0`
`x^2-7x+10=0`
Láthatod, itt is szinte ugyanaz jött ki, csak -1-egy megszorozva, ami másodfokú esetén nem számít.
Tehát, akármit írsz eredetileg az `a`, `b`, `c` helyére, ha leegyszerűsíted a végén csak kettő marad (egymás ellentettei).
És ezt megcsinálhatod a többinél is, nekem már nincs rá időm.
1
- Még nem érkezett komment!
 RationalRick
{ Fizikus }
válasza
RationalRick
{ Fizikus }
válasza
Ja, még annyit, hogy ezeket egyszerűbben is meg lehet oldani, a gyöktényezős alak segítségével, és akkor nem kell a Viète-formulákat használni, de mivel ez volt a feladat címe, ezért így csináltam.
De akkor most megmutatom a gyöktényezős alakkal is:
`x_1=5`
`x_2=2`
Felírható úgy, hogy:
`(x-5)(x-2)=0`
Felbontom a zárójelet:
`x^2-5x-2x+10=0`
`x^2-7x+10=0`
És ki is jött ugyanez.
De akkor most megmutatom a gyöktényezős alakkal is:
`x_1=5`
`x_2=2`
Felírható úgy, hogy:
`(x-5)(x-2)=0`
Felbontom a zárójelet:
`x^2-5x-2x+10=0`
`x^2-7x+10=0`
És ki is jött ugyanez.
1
- Még nem érkezett komment!
 RationalRick
{ Fizikus }
válasza
RationalRick
{ Fizikus }
válasza
3. kép
Itt meg kell vizsgálni a diszkriminánst. Ha nagyobb, mint nulla, akkor két megoldása van, ha nulla, akkor egy (azaz kettő egyenlő) és ha kisebb, mint nulla, akkor pedig nincs valós megoldása.
A diszkrimináns:
`color(blue)(D=b^2-4ac)`
`a)`
`6x^2+7x+1`
`D=7^2-4*6*1=25`
`D>0`
2 valós gyök
`b)`
`6x^2+7x+5`
`D=7^2-4*6*5=-71`
`D<0`
nincs valós gyök
`c)`
`-3x^2-4x-2=0`
`D=(-4)^2-4*(-3)*(-2)=-8`
`D<0`
nincs valós gyök
`d)`
`-x^2+10x-25=0`
`D=10^2-4*(-1)*(-25)=0`
`D=0`
egy valós gyök
`e)`
`2x^2-4x+2=0`
`D=(-4)^2-4*2*2=0`
`D=0`
egy valós gyök
`f)`
`-3x^2+4x+2=0`
`D=4^2-4*(-3)*2=40`
`D>0`
két valós gyök
Itt meg kell vizsgálni a diszkriminánst. Ha nagyobb, mint nulla, akkor két megoldása van, ha nulla, akkor egy (azaz kettő egyenlő) és ha kisebb, mint nulla, akkor pedig nincs valós megoldása.
A diszkrimináns:
`color(blue)(D=b^2-4ac)`
`a)`
`6x^2+7x+1`
`D=7^2-4*6*1=25`
`D>0`
2 valós gyök
`b)`
`6x^2+7x+5`
`D=7^2-4*6*5=-71`
`D<0`
nincs valós gyök
`c)`
`-3x^2-4x-2=0`
`D=(-4)^2-4*(-3)*(-2)=-8`
`D<0`
nincs valós gyök
`d)`
`-x^2+10x-25=0`
`D=10^2-4*(-1)*(-25)=0`
`D=0`
egy valós gyök
`e)`
`2x^2-4x+2=0`
`D=(-4)^2-4*2*2=0`
`D=0`
egy valós gyök
`f)`
`-3x^2+4x+2=0`
`D=4^2-4*(-3)*2=40`
`D>0`
két valós gyök
Módosítva: 2 éve
1
- Még nem érkezett komment!
 RationalRick
{ Fizikus }
megoldása
RationalRick
{ Fizikus }
megoldása
4. kép
Szintén a gyöktényezős alakot használjuk.
`a)`
`x^2-2x-3=0`
`x_1=-1`
`x_2=3`
Tehát ez `(x+1)(x-3)` lesz.
`d)`
`-20x^2+7x+6=0`
`x_1=-2/5`
`x_2=3/4`
Ez pedig:
`-20(x+2/5)(x-3/4)`
`-(5x+2)(4x-3)`
A többit ez alapján már meg tudod csinálni.
Szintén a gyöktényezős alakot használjuk.
`a)`
`x^2-2x-3=0`
`x_1=-1`
`x_2=3`
Tehát ez `(x+1)(x-3)` lesz.
`d)`
`-20x^2+7x+6=0`
`x_1=-2/5`
`x_2=3/4`
Ez pedig:
`-20(x+2/5)(x-3/4)`
`-(5x+2)(4x-3)`
A többit ez alapján már meg tudod csinálni.

1
-
Ármós Csaba: Ügyi vagy, Rick, gratula!
 2 éve
0
2 éve
0
-
RationalRick: Köszi!
 2 éve
0
2 éve
0