Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Szöveges feladat
 Törölt
kérdése
Törölt
kérdése
400
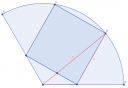
Egy 120°-os körcikk alakú telekre olyan négyzet alapterületű házat szeretnénk építeni, amelynek két csúcsa a körcikk egy-egy sugarára, másik két csúcsa pedig a határoló körívre illeszkedik. Egy helyi szabvány szerint a telekre csak olyan ház építhető, melynek alapterülete nem haladja meg a telek területének 50%-át. Megépíthetjük-e ezt a házat?
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Középiskola / Matematika
Válaszok
1 bazsa990608
{ Közgazdász }
megoldása
bazsa990608
{ Közgazdász }
megoldása
Először is a fő probléma, hogy nem tudjuk a négyzet oldalának hosszát ezért valahogyan meg kéne határozzuk. Nézzük meg miket tudunk kapsából kiszámolni és, hogy azokkal hogyan tudunk tovább haladni a megoldás felé.
Biztos, hogy `"DOA"` háromszög egyenlő szárú háromszög melynek O csúcsban lévő szöge `120°` Tehát: `DhatOA=120°`
Ebből adódóan mivel az egyenlő szárú háromszög alapon fekvő szögei megegyeznek megkaphatjuk, hogy mekkora szöget zár be `"A"` csúcs azaz: `ThatAO=(180°-120°)/2=color(red)(30°)`
Mivel `"BAT"` derékszögű háromszög és `"A"` csúcsnál helyezkezdik el a derékszög. Így tudjuk,hogy `BhatAO=30°+90°=color(red)(120°)`.
Ezen adatok ismeretében már felírhatunk egy coszinusz tételt. Mely: `"OB"^2=x^2+"AO"^2-2*x*"AO"*cos120°`
Ebből az egyenletből nem ismerünk még sok mindent. De határozzuk meg őket egyesével.
`"AO"` szakaszra felírhatunk egy coszinusz szögfüggvényt melyből: `cos30°=(x/2)/("OA")=>sqrt3/2=x/(2"OA")=>"OA"=x/sqrt3`
`cos120°=-1/2`
Helyettesítsünk a coszinusz tételünkbe úgy, hogy a körcikk sugarát tekintsük 1 egységnek az egyszerűség kedvéért. Azt kapjuk, hogy: `1=x^2+(x/sqrt3)^2-2*(x/sqrt3)^2*(-1/2)` Ahonnan: `x^2=3/(4+sqrt3)=(3*(4-sqrt3))/13`
A körcikk terület `(1^2*pi*120°)/(360°)=pi/3`
A két terület aránya: `((3*(4-sqrt3))/13)/(pi/3)approx0,499` Tehát megépíthető a ház éppen hogy csak.
Biztos, hogy `"DOA"` háromszög egyenlő szárú háromszög melynek O csúcsban lévő szöge `120°` Tehát: `DhatOA=120°`
Ebből adódóan mivel az egyenlő szárú háromszög alapon fekvő szögei megegyeznek megkaphatjuk, hogy mekkora szöget zár be `"A"` csúcs azaz: `ThatAO=(180°-120°)/2=color(red)(30°)`
Mivel `"BAT"` derékszögű háromszög és `"A"` csúcsnál helyezkezdik el a derékszög. Így tudjuk,hogy `BhatAO=30°+90°=color(red)(120°)`.
Ezen adatok ismeretében már felírhatunk egy coszinusz tételt. Mely: `"OB"^2=x^2+"AO"^2-2*x*"AO"*cos120°`
Ebből az egyenletből nem ismerünk még sok mindent. De határozzuk meg őket egyesével.
`"AO"` szakaszra felírhatunk egy coszinusz szögfüggvényt melyből: `cos30°=(x/2)/("OA")=>sqrt3/2=x/(2"OA")=>"OA"=x/sqrt3`
`cos120°=-1/2`
Helyettesítsünk a coszinusz tételünkbe úgy, hogy a körcikk sugarát tekintsük 1 egységnek az egyszerűség kedvéért. Azt kapjuk, hogy: `1=x^2+(x/sqrt3)^2-2*(x/sqrt3)^2*(-1/2)` Ahonnan: `x^2=3/(4+sqrt3)=(3*(4-sqrt3))/13`
A körcikk terület `(1^2*pi*120°)/(360°)=pi/3`
A két terület aránya: `((3*(4-sqrt3))/13)/(pi/3)approx0,499` Tehát megépíthető a ház éppen hogy csak.
1
-
VF: Ügyes. Az ábra is. Mivel csináltad? 2 éve 0
-
bazsa990608: https://www.geogebra.org/calculator 2 éve 1