Toplista
- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Matek házi
Nayaaa
kérdése
1149
1)Egy derékszögű háromszög átfogójának hossza 5 dm, egyik befogójának hossza 48 cm. Határozd meg a távolságot a háromszög súlypontja és a köré írható körének középpontja között, valamint a háromszög súlypontja és magasságpontja között!
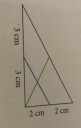
2) Az ábra szerinti derékszögű háromszögben a derékszögü csúcsot összekötöttük az átfogó felezőpontjával, és összekötöttüka két befogó felezőpontját is. Mekkora ez a két szakasz?
2) Az ábra szerinti derékszögű háromszögben a derékszögü csúcsot összekötöttük az átfogó felezőpontjával, és összekötöttüka két befogó felezőpontját is. Mekkora ez a két szakasz?
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Középiskola / Matematika
Válaszok
1
bazsa990608
{ Közgazdász }
megoldása
1.)
Másik befogó hossza: `b=sqrt(c^2-a^2)=sqrt(50^2-48^2)=color(red)(14 \ cm)`
A súlyvonalak felezik a derékszögű háromszög oldalainak hosszát ezzel egyenlőszárú háromszögeket hozva létre. Valamint azt is tudjuk, hogy a súlyvonalak 2:1 arányban osztják fel egymást a súlypontban.
A derékszögű háromszög köré írható kör sugara megegyezik a derékszögű háromszög átfogójának felével. Tehát ebből megállapíthatjuk, hogy a súlypont és a köréírható kör középpontájnak távolsága az `1/3` része az átfogóval szembeni szögből induló súlyvonal hosszával.
A súlyvonal megegyezik derékszögű háromszög köré írható kör sugarával tehát a két középpont távolsága: `50*1/3=color(red)(16,67 \ cm)`
Nem méretarányos ábra a szemléltetés céljából: https://www.geogebra.org/calculator/vcgcngv9
2.)
A kék vonal hossza: `k=sqrt(3^2+2^2)=color(red)(3,61 \ cm)`
A zöld vonal hossza: `z=(sqrt((2*3)^2+(2*2)^2))/2=color(red)(3,61 \ cm)`
Másik befogó hossza: `b=sqrt(c^2-a^2)=sqrt(50^2-48^2)=color(red)(14 \ cm)`
A súlyvonalak felezik a derékszögű háromszög oldalainak hosszát ezzel egyenlőszárú háromszögeket hozva létre. Valamint azt is tudjuk, hogy a súlyvonalak 2:1 arányban osztják fel egymást a súlypontban.
A derékszögű háromszög köré írható kör sugara megegyezik a derékszögű háromszög átfogójának felével. Tehát ebből megállapíthatjuk, hogy a súlypont és a köréírható kör középpontájnak távolsága az `1/3` része az átfogóval szembeni szögből induló súlyvonal hosszával.
A súlyvonal megegyezik derékszögű háromszög köré írható kör sugarával tehát a két középpont távolsága: `50*1/3=color(red)(16,67 \ cm)`
Nem méretarányos ábra a szemléltetés céljából: https://www.geogebra.org/calculator/vcgcngv9
2.)
A kék vonal hossza: `k=sqrt(3^2+2^2)=color(red)(3,61 \ cm)`
A zöld vonal hossza: `z=(sqrt((2*3)^2+(2*2)^2))/2=color(red)(3,61 \ cm)`
1
- Még nem érkezett komment!