Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Valaki el tudná magyarázni nekem érthetően ezt a feladatot?
 Benedek Balázs
kérdése
Benedek Balázs
kérdése
276
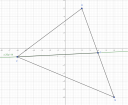
Csatoltam képet.
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Középiskola / Matematika
Válaszok
1 bazsa990608
{ Közgazdász }
megoldása
bazsa990608
{ Közgazdász }
megoldása
a.)
Mint tudjuk a súlyvonal felezi az oldalt így elöször is megkell határozzuk `RQ` szakasz felezópontjának koordinátáit.
`F((6+2)/2;(-6+5)/2)=color(red)(F(4;-1/2))`
Majd meghatározzuk a súlyvonal irányvektorát.
`vec(PF)=(4-(-6);-1/2-(-1))=color(red)("(10;0,5)")`
Majd egyszerűen csak behelyettesítünk a képletbe.
`v_2*x-v_1*y=v_2*x_0-v_1*y_0`
`0,5x-10y=0,5*(-6)-10*(-1)`
`color(red)(x-20y=14)` Ez a súlyvonal egyenlete.
b.)
Meghatározzuk az egyes szakaszok hosszait majd cosinusz tétel használatával kiszámoljuk a kívánt szöget.
`PR=sqrt((P_1-R_1)^2+(P_2-R_2)^2)=sqrt((-6-2)^2+(-1-5)^2)=10 \ cm`
`PQ=sqrt((P_1-Q_1)^2+(P_2-Q_2)^2)=sqrt((-6-6)^2+(-1-(-6))^2)=13 \ cm`
`RQ=sqrt((R_1-Q_1)^2+(R_2-Q_2)^2)=sqrt((2-6)^2+(5-(-6))^2)=sqrt137 \ cm`
`cosalpha=(sqrt137^2-(10^2+13^2))/(-2*10*13)=>color(red)(alpha=59,49°)`
Mint tudjuk a súlyvonal felezi az oldalt így elöször is megkell határozzuk `RQ` szakasz felezópontjának koordinátáit.
`F((6+2)/2;(-6+5)/2)=color(red)(F(4;-1/2))`
Majd meghatározzuk a súlyvonal irányvektorát.
`vec(PF)=(4-(-6);-1/2-(-1))=color(red)("(10;0,5)")`
Majd egyszerűen csak behelyettesítünk a képletbe.
`v_2*x-v_1*y=v_2*x_0-v_1*y_0`
`0,5x-10y=0,5*(-6)-10*(-1)`
`color(red)(x-20y=14)` Ez a súlyvonal egyenlete.
b.)
Meghatározzuk az egyes szakaszok hosszait majd cosinusz tétel használatával kiszámoljuk a kívánt szöget.
`PR=sqrt((P_1-R_1)^2+(P_2-R_2)^2)=sqrt((-6-2)^2+(-1-5)^2)=10 \ cm`
`PQ=sqrt((P_1-Q_1)^2+(P_2-Q_2)^2)=sqrt((-6-6)^2+(-1-(-6))^2)=13 \ cm`
`RQ=sqrt((R_1-Q_1)^2+(R_2-Q_2)^2)=sqrt((2-6)^2+(5-(-6))^2)=sqrt137 \ cm`
`cosalpha=(sqrt137^2-(10^2+13^2))/(-2*10*13)=>color(red)(alpha=59,49°)`
0
- Még nem érkezett komment!