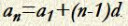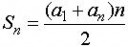Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Mi a sorozat általános képlete?
 Hipocentrum
kérdése
Hipocentrum
kérdése
734
A sorozat egyszerűen ismétli az 1, 2, 3 számokat, tehát a1=a4=a7 (stb.)=1; a2=a5=8 (stb.)=2; a3=a6=a9 (stb.)=3;
Mi a sorozat n-edik tagját meghatározó explicit képlet, és mi a sorozat Sn összegét adó képlet (Sn=a1+a2+3+...+an)?
Mi a sorozat n-edik tagját meghatározó explicit képlet, és mi a sorozat Sn összegét adó képlet (Sn=a1+a2+3+...+an)?
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Középiskola / Matematika
Válaszok
3 Pithagorasz
válasza
Pithagorasz
válasza
A számtani sorozat n-edik tagját meghatározó képlet az 1. kép.
A számtani sorozat Sn összegét adó képlet a 2. kép.
A számtani sorozat Sn összegét adó képlet a 2. kép.
0
- Még nem érkezett komment!
 Hipocentrum
válasza
Hipocentrum
válasza
Kedves Pithagorasz!
Számtani sorozatnak nevezzük azt a sort, amelynek n-edik eleméből (n-1)-edik elemét kivonva d-t kapunk. A fenti sorozatra ez nem igaz (sem a mértani sorozat leírása).
Számtani sorozatnak nevezzük azt a sort, amelynek n-edik eleméből (n-1)-edik elemét kivonva d-t kapunk. A fenti sorozatra ez nem igaz (sem a mértani sorozat leírása).
0
- Még nem érkezett komment!
 Rantnad
{
Rantnad
{  }
megoldása
}
megoldása
Első körben érdemes olyan sorozatot keresni, ami egyáltalán periodikusan veszi fel az értékeket, én példának okáért ezt találtam: sin(n*120°), ahol n természetes szám, de nem 0. Ez a sorozat ezeket az értékeket fogja felvenni: √3/2; -√3/2; 0; ... Ha a sorozatot osztjuk √3/2-vel, akkor az értékek így követik egymást: 1; -1; 0; ... Most toljuk el a sorozatot 1 taggal hátra, ekkor ezt kapjuk: -1; 0; 1; ..., ha ehhez hozzáadunk 2-t, ezt a sorozatot kapjuk: 1; 2; 3; ... Tehát a
2+(sin((n+1)*120°)/(√3/2)) egy megfelelő sorozat lesz. Ha valaki jobban szereti a radiánt, átírhatja a szöget:
2+(sin((n+1)*(2π/3)/(√3/2)), ez rendre az 1; 2; 3; ... tagokat fogja felvenni.
Összegre egyelőre ezt a képletet tudom adni:
[(n+2)/3]*1+[(n+1)/3]*2+[n/3]*3, , ahol "[ ]" a szám alsó egész részét jelöli. Lehet, hogy van ennél egyszerűbb és szebb összegképlet is, egyelőre ez van.
2+(sin((n+1)*120°)/(√3/2)) egy megfelelő sorozat lesz. Ha valaki jobban szereti a radiánt, átírhatja a szöget:
2+(sin((n+1)*(2π/3)/(√3/2)), ez rendre az 1; 2; 3; ... tagokat fogja felvenni.
Összegre egyelőre ezt a képletet tudom adni:
[(n+2)/3]*1+[(n+1)/3]*2+[n/3]*3, , ahol "[ ]" a szám alsó egész részét jelöli. Lehet, hogy van ennél egyszerűbb és szebb összegképlet is, egyelőre ez van.
Módosítva: 9 éve
0
- Még nem érkezett komment!