Először is számoljuk ki a derékszögű háromszög két befogójának a hosszát.

`20=sqrt(x^2+(sqrt3x)^2)`

`400=x^2+3x^2`

`400=4x^2`

`100=x^2`

`color(red)(10=x)`



Egyik befogó: `a=x=color(red)(10 \ cm)`

Másik befogó: `b=sqrt3x=sqrt3*10=color(red)(17,32 \ cm)`



A derékszögű háromszög köré írható kör sugara megegyezik a derékszögű háromszög átfogójának felvével. Tehát: `r=c/2=20/2=color(red)(10 \ cm)`

`T_("köréírt kör")=r^2*pi=10^2*pi=color(red)(314,16 \ cm^2)`

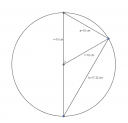
A képen jól látható, hogy a legrövidebb befogó a sugárral egy szabályos háromszöget alkot melynek belső szögei mind 60°-osak.

Ki kell számolnunk a legrövidebb befogó által elválasztott körszelet területét majd kivonni a teljes kör területéből. Így megkapva a két keresett terület nagyságát

`T_("körszelet")=((r^2*pi*alpha)/(180°))/2-(r^2*sinalpha)/2=((10^2*pi*60°)/(180°))/2-(10^2*sin60°)/2=color(red)(9,06 \ cm^2)`


Kisebbik rész területe: `T_("körszelet")=color(red)(ul(9,06 \ cm^2))`

Nagyobbik rész területe: `T_("köréírt kör")- T_("körszelet")=314,16-9,06=color(red)(ul(305,1 \ cm^2))`