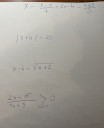Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Feladat
 zolifc
kérdése
zolifc
kérdése
271
Sziasztok, valaki meg tudná nekem ezeket oldani?
Előre is köszönöm!
Előre is köszönöm!
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Középiskola / Matematika
Válaszok
1 kazah
megoldása
kazah
megoldása
1,
`x-(6-x)/7=2x-4-(x+3)/3`
szorzunk a közös nevezővel (21):
`21x-3(6-x)=21(2x-4)-7(x+3)`
zárójelbontás
`21x-18+3x=42x-84-7x-21`
összevonás
`24x-18=35x-105` /-24x
-18=11x-105 /+105
11x=87 /:12
`x=87/11`
Ellenőrzés!
2,
`|x+4|=20`
I. Ha x+4 = 20, akkor
`x_1=16`
II. Ha x+4 = -20, akkor
`x_2=-24`
3,
`x-4=root()(x+2)`
Felt: `x le -2`
emeljünk négyzetre
`(x-4)^2=x+2`
`x^2-8x+16=x+2`
`x^2-9x+14=0`
`x_(1,2)=(9 pm root()(9^2-4*14))/2` = `(9 pm 5)/2`
`x_1=7`
`x_2=2`
Ellenőrizni mindenképpen kell, mert a négyzetreemelés miatt felléphetett gyökszaporulat.
Az x = 2 nem megoldás, csak az `ul("x = 7")`.
`(2x-15)/(3x+9) le 0`
Felt: `x ne -3` (a nevező nem lehet nulla)
Tört értéke akkor nagyobb-egyenlő nulla, ha
I. A számláló nemnegatív és a nevező pozitív
`2x-15 ge 0` `cap` `3x+9 gt 0`
`x ge 15/2` `cap` `x gt -3` `to` `x ge 15/2`
II. A számláló kisebb-egyenlő nulla és a nevező negatív:
`2x-15 le 0` `cap` `3x+9 lt 0`
`x le 15/2` `cap` `x lt -3` `to` `x lt -3`
Megoldás: `x in RR` ; `x in "]"-oo;-3"[" cap "["15/2;oo[`
-3-nál kisebb és `15/2` vagy nagyobb számok esetén.
Az ellenőrzés el kell végezni
1. -3-nál kisebb számra (igaz)
2. (-3-ra nem kell, ott nincs megoldás)
3. -3 és `15/2` közötti értékre (pl. 0-ra, hamis lesz)
4. `15/2`-re (igaz)
5. `15/2`-nél nagyobbra (igaz)
`x-(6-x)/7=2x-4-(x+3)/3`
szorzunk a közös nevezővel (21):
`21x-3(6-x)=21(2x-4)-7(x+3)`
zárójelbontás
`21x-18+3x=42x-84-7x-21`
összevonás
`24x-18=35x-105` /-24x
-18=11x-105 /+105
11x=87 /:12
`x=87/11`
Ellenőrzés!
2,
`|x+4|=20`
I. Ha x+4 = 20, akkor
`x_1=16`
II. Ha x+4 = -20, akkor
`x_2=-24`
3,
`x-4=root()(x+2)`
Felt: `x le -2`
emeljünk négyzetre
`(x-4)^2=x+2`
`x^2-8x+16=x+2`
`x^2-9x+14=0`
`x_(1,2)=(9 pm root()(9^2-4*14))/2` = `(9 pm 5)/2`
`x_1=7`
`x_2=2`
Ellenőrizni mindenképpen kell, mert a négyzetreemelés miatt felléphetett gyökszaporulat.
Az x = 2 nem megoldás, csak az `ul("x = 7")`.
`(2x-15)/(3x+9) le 0`
Felt: `x ne -3` (a nevező nem lehet nulla)
Tört értéke akkor nagyobb-egyenlő nulla, ha
I. A számláló nemnegatív és a nevező pozitív
`2x-15 ge 0` `cap` `3x+9 gt 0`
`x ge 15/2` `cap` `x gt -3` `to` `x ge 15/2`
II. A számláló kisebb-egyenlő nulla és a nevező negatív:
`2x-15 le 0` `cap` `3x+9 lt 0`
`x le 15/2` `cap` `x lt -3` `to` `x lt -3`
Megoldás: `x in RR` ; `x in "]"-oo;-3"[" cap "["15/2;oo[`
-3-nál kisebb és `15/2` vagy nagyobb számok esetén.
Az ellenőrzés el kell végezni
1. -3-nál kisebb számra (igaz)
2. (-3-ra nem kell, ott nincs megoldás)
3. -3 és `15/2` közötti értékre (pl. 0-ra, hamis lesz)
4. `15/2`-re (igaz)
5. `15/2`-nél nagyobbra (igaz)
0
-
kazah: a 3. feladatnál a feltétel nagyobb-egyenlő 2 éve 0