Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
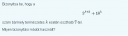
Bizonyítsa be, hogy a szám bármely természetes k esetén osztható 7-tel.
 pappmarton02
kérdése
pappmarton02
kérdése
334
Ezt és az ilyen típusú bizonyításokat hogyan kell elvégezni?
Válaszokat előre is köszönöm
Válaszokat előre is köszönöm

Jelenleg 1 felhasználó nézi ezt a kérdést.
bizonyítás, oszthatóság
bizonyítás, oszthatóság
0
Középiskola / Matematika
Válaszok
1 kormosmate2
válasza
kormosmate2
válasza
A feladatot kétféleképpen is megoldhatjuk.
Első megoldás:
Teljes indukcióval bizonyítunk. Ennek lényege, hogy először belátjuk, hogy az állítás igaz a változó (k) legkisebb megengedett értékére, majd feltesszük, hogy tetszőleges k értékre is igaz, és bebizonyítjuk, hogy ebből következik, hogy k+1-re is igaz lesz, így k minden lehetséges értékére beláttuk az állítást. Megjegyzés, az oszthatóság jele: |. Pl. `3|12` olvasd, 3 osztja a 12-t.
1) `k=1`:
`3^{1+3}+10^1 = 81+10=91`
`7|91` mert `91=7*13`
Tehát az állítás k=1-re igaz.
2) `k\in\mathbb{N}`:
`7|3^{k+3}+10^k`
3) `(k+1)\in\mathbb{N}`:
Ebben a lépésben az a célunk, hogy a k+1-es kifejezésben kialakítsuk 2)-t, mert ez az, amiről feltettük, hogy igaz, és fel akarjuk használni 3)-ban:
`3^{(k+1)+3}+10^{k+1} = 3*3^{k+3}+10*10^k = 3^{k+3}+3*10^k+7*10^k = 3*\underbrace{(3^{k+3}+10^k)}_{7|}+7*10^k`
Az összeg első tagjában a zárójeles tényező 2) miatt osztható 7-el, így a 3-szorosa is, az összeg másik tagja pedig 7 többszöröse, így az is osztható 7-el. Mivel az összeg mindkét tagja osztható 7-el, így az egész is, ezzel a bizonyítás kész.
Második megoldás:
Ez kicsit rövidebb, ezt azért tudjuk alkalmazni, mert a bizonyítandó kifejezésben két különböző exponenciális tag is van, egyébként csak az első út lenne járható. Ehhez a következő összefüggést kell tudnunk:
`a-b|a^n-b^n`
Azaz két szám ugyanolyan hatványának a különbsége mindig osztható a két szám különbségével. Ehhez előbb kicsit átalakítunk:
`3^{k+3}+10^k = 10^k+27*3^k = 10^k-3^k+28*3^k`
A különbség osztható 7-el, mivel `7=10-3|10^k-3^k`, az összeg másik része pedig 28 többszöröse, és mivel 28 osztható 7-el, így 28 minden többszöröse is osztható 7-el. Az összeg mindkét része osztható 7-el, így az egész is, ezzel az állítást bizonyítottuk.
Első megoldás:
Teljes indukcióval bizonyítunk. Ennek lényege, hogy először belátjuk, hogy az állítás igaz a változó (k) legkisebb megengedett értékére, majd feltesszük, hogy tetszőleges k értékre is igaz, és bebizonyítjuk, hogy ebből következik, hogy k+1-re is igaz lesz, így k minden lehetséges értékére beláttuk az állítást. Megjegyzés, az oszthatóság jele: |. Pl. `3|12` olvasd, 3 osztja a 12-t.
1) `k=1`:
`3^{1+3}+10^1 = 81+10=91`
`7|91` mert `91=7*13`
Tehát az állítás k=1-re igaz.
2) `k\in\mathbb{N}`:
`7|3^{k+3}+10^k`
3) `(k+1)\in\mathbb{N}`:
Ebben a lépésben az a célunk, hogy a k+1-es kifejezésben kialakítsuk 2)-t, mert ez az, amiről feltettük, hogy igaz, és fel akarjuk használni 3)-ban:
`3^{(k+1)+3}+10^{k+1} = 3*3^{k+3}+10*10^k = 3^{k+3}+3*10^k+7*10^k = 3*\underbrace{(3^{k+3}+10^k)}_{7|}+7*10^k`
Az összeg első tagjában a zárójeles tényező 2) miatt osztható 7-el, így a 3-szorosa is, az összeg másik tagja pedig 7 többszöröse, így az is osztható 7-el. Mivel az összeg mindkét tagja osztható 7-el, így az egész is, ezzel a bizonyítás kész.
Második megoldás:
Ez kicsit rövidebb, ezt azért tudjuk alkalmazni, mert a bizonyítandó kifejezésben két különböző exponenciális tag is van, egyébként csak az első út lenne járható. Ehhez a következő összefüggést kell tudnunk:
`a-b|a^n-b^n`
Azaz két szám ugyanolyan hatványának a különbsége mindig osztható a két szám különbségével. Ehhez előbb kicsit átalakítunk:
`3^{k+3}+10^k = 10^k+27*3^k = 10^k-3^k+28*3^k`
A különbség osztható 7-el, mivel `7=10-3|10^k-3^k`, az összeg másik része pedig 28 többszöröse, és mivel 28 osztható 7-el, így 28 minden többszöröse is osztható 7-el. Az összeg mindkét része osztható 7-el, így az egész is, ezzel az állítást bizonyítottuk.
Módosítva: 3 éve
0
- Még nem érkezett komment!