Toplista
- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Befogó, és magasságtétel
elecs6002
kérdése
302
A derékszögű háromszög befogói úgy aránylanak egymáshoz, mint 3:7. Az átfogóhoz tartozó magasság hossza 42cm. Hogy kéne elkezdenem, ebből kiszámítsam az átfogó hosszát? Előre is köszi!
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Középiskola / Matematika
Válaszok
1
kazah
válasza
Ha nem nagyon erőlteted a magasságtételt, akkor a logika is segít.
Ábra
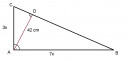
A derékszögű háromszögben a két befogó hosszát jelölheted 3x és 7x cm-rel.
Az átfogó hosszát ki tudod számolni (paraméteresen):
`bar(BC)` = `root()((3x)^2+(7x)^2)` = `root()(58)*x`
Ha berajzolod a magasságot, rögtön lesz három darab hasonló háromszöged, melyben a megfelelő oldalak aránya egyenlő.
`(AD)/(AC)=(AB)/(BC)`
`42/(3x)=(7x)/(root()(58)*x)`
`x=(root()(58))/(7*3)*42` = `2*root()(58)`
Az átfogó tehát:
`bar(BC)` = `root()(58)*(2*root()(58))` = `58*2` = `ul("116 cm")`.
Leellenőrizzük területre:
`T=((AB)*(AC))/2` = `((3*2*root()(58))*(7*2*root()(58)))/2` = `42*58` = 2436 `cm^2`
`T=((BC)*(AD))/2` = `(116*42)/2` = 2436 `cm^2`
Ábra
A derékszögű háromszögben a két befogó hosszát jelölheted 3x és 7x cm-rel.
Az átfogó hosszát ki tudod számolni (paraméteresen):
`bar(BC)` = `root()((3x)^2+(7x)^2)` = `root()(58)*x`
Ha berajzolod a magasságot, rögtön lesz három darab hasonló háromszöged, melyben a megfelelő oldalak aránya egyenlő.
`(AD)/(AC)=(AB)/(BC)`
`42/(3x)=(7x)/(root()(58)*x)`
`x=(root()(58))/(7*3)*42` = `2*root()(58)`
Az átfogó tehát:
`bar(BC)` = `root()(58)*(2*root()(58))` = `58*2` = `ul("116 cm")`.
Leellenőrizzük területre:
`T=((AB)*(AC))/2` = `((3*2*root()(58))*(7*2*root()(58)))/2` = `42*58` = 2436 `cm^2`
`T=((BC)*(AD))/2` = `(116*42)/2` = 2436 `cm^2`
0
- Még nem érkezett komment!