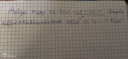Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Differenciahányados számolás
 bdani040110
kérdése
bdani040110
kérdése
348
Sziasztok! Valaki tudna segíteni hogy ezt hogy kell megoldani? Csütörtökön vizsgám lesz és arra szeretném begyakorolni.
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Felsőoktatás / Matematika
Válaszok
1 gyula205
megoldása
gyula205
megoldása
Deriválod a megadott függvényt is behelyettesíted a `(-1)`-et.
Mi ebben a nehézség?
Használd a függvények hányadosára vonatkozó derivációs szabályt!
`f'(x)=frac{3(2x^4-2x+1)}{x^4}`.
`f'(-1)=15`.
Most látom, hogy nem diffrenciálhányadosról, hanem differenciahányadosról van szó.
A differenciahányados értéke nemcsak `x_0`-tól hanem változó `Deltax` növekményétől is függ.
Tehát javításra szorul a példa megoldása.
`frac{Deltay}{Deltax}=frac{f(x+Deltax)-f(x)}{Deltax}`
Ebből fog kelleni a `6(x+Deltax)^4+3(x+Deltax)-1` kiszámítása.
`6(x+Deltax)^4+3(x+Deltax)-1=6·x^4 + 24·(Deltax)·x^3 + 36·(Deltax)^2·x^2 + 24·(Deltax)^3·x + 6·(Deltax)^4+3(x+Deltax)-1`.
`f(x+Deltax)=frac{(6·x^4 + 24·Deltax·x^3 + 36·(Deltax)^2·x^2 + 3·x·(8·(Deltax)^3 + 1) + 6·(Deltax)^4 + 3·Deltax - 1)}{(x+Deltax)^3}`.
Legyen `A(x, b)=6·x^6 + 18·b·x^5 + 18·b^2·x^4 + x^3·(6·b^3 - 6)` és
`B(x, b)=3·x^2·(1 - 3·b) + 3·b·x·(1 - b) + b^2`.
Ekkor `f(x+b)-f(b)=frac{b(A(x,b)+B(x,b))}{x^3(x+b)^3}`.
Így `frac{f(x+b)-f(b)}{b}=frac{(A(x,b)+B(x,b))}{x^3(x+b)^3}`.
A `b=Deltax` helyettesítés után `frac{f(x+Deltax)-f(Deltax)}{Deltax}=frac{(A(x,Deltax)+B(x,Deltax))}{x^3(x+Deltax)^3}`.
Majd elvégezve az `x=-1` helyettesítést adódik, hogy
`frac{Deltay}{Deltax}=frac{f(-1+Deltax)-f(Deltax)}{Deltax}=frac{(Deltax)^3-22(Deltax)^2+30*Deltax-15}{(Deltax-1)^3}`.
Relatív ellenőrzés: Ha `Deltax->0`, akkor a derivált értéke `15`. (Lásd az első sorokban található levezetést.)
Mi ebben a nehézség?
Használd a függvények hányadosára vonatkozó derivációs szabályt!
`f'(x)=frac{3(2x^4-2x+1)}{x^4}`.
`f'(-1)=15`.
Most látom, hogy nem diffrenciálhányadosról, hanem differenciahányadosról van szó.
A differenciahányados értéke nemcsak `x_0`-tól hanem változó `Deltax` növekményétől is függ.
Tehát javításra szorul a példa megoldása.
`frac{Deltay}{Deltax}=frac{f(x+Deltax)-f(x)}{Deltax}`
Ebből fog kelleni a `6(x+Deltax)^4+3(x+Deltax)-1` kiszámítása.
`6(x+Deltax)^4+3(x+Deltax)-1=6·x^4 + 24·(Deltax)·x^3 + 36·(Deltax)^2·x^2 + 24·(Deltax)^3·x + 6·(Deltax)^4+3(x+Deltax)-1`.
`f(x+Deltax)=frac{(6·x^4 + 24·Deltax·x^3 + 36·(Deltax)^2·x^2 + 3·x·(8·(Deltax)^3 + 1) + 6·(Deltax)^4 + 3·Deltax - 1)}{(x+Deltax)^3}`.
Legyen `A(x, b)=6·x^6 + 18·b·x^5 + 18·b^2·x^4 + x^3·(6·b^3 - 6)` és
`B(x, b)=3·x^2·(1 - 3·b) + 3·b·x·(1 - b) + b^2`.
Ekkor `f(x+b)-f(b)=frac{b(A(x,b)+B(x,b))}{x^3(x+b)^3}`.
Így `frac{f(x+b)-f(b)}{b}=frac{(A(x,b)+B(x,b))}{x^3(x+b)^3}`.
A `b=Deltax` helyettesítés után `frac{f(x+Deltax)-f(Deltax)}{Deltax}=frac{(A(x,Deltax)+B(x,Deltax))}{x^3(x+Deltax)^3}`.
Majd elvégezve az `x=-1` helyettesítést adódik, hogy
`frac{Deltay}{Deltax}=frac{f(-1+Deltax)-f(Deltax)}{Deltax}=frac{(Deltax)^3-22(Deltax)^2+30*Deltax-15}{(Deltax-1)^3}`.
Relatív ellenőrzés: Ha `Deltax->0`, akkor a derivált értéke `15`. (Lásd az első sorokban található levezetést.)
Módosítva: 3 éve
1
-
bdani040110: Az a baj, hogy a feladat teljes szövege ennyi és nem ír semmilyen növekményről 3 éve 0
-
gyula205: Az nem baj, csak a megoldásodban fel kell tüntetni a növekményt. Növekmény függvényében két harmadfokú polinom hányadosa a megoldás. 3 éve 0
-
bdani040110: Köszönöm szépen az eddigit! 3 éve 0
-
bdani040110: Köszönöm szépen! 3 éve 0