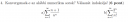Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Sorok Konvergenciája
 ZS0fi19
kérdése
ZS0fi19
kérdése
372
Sziasztok! A lenti feladatban szeretnék segítséget kérni, hogy hogyan kell megoldani. Nagyon megköszönném, ha érthetően levezetné valaki, mert így könnyebben tudom megérteni az ilyen típusú feladatokat.
Jelenleg 1 felhasználó nézi ezt a kérdést.
#matematika, #Konvergencia, #Sorok
#matematika, #Konvergencia, #Sorok
0
Középiskola / Matematika
Válaszok
3 gyula205
megoldása
gyula205
megoldása
b.) sor abszolút konvergens. Ugyanis használható a `sum_(n=1)^(oo) a_n` alakú sorra a hányadoskritérium (https://en.wikipedia.org/wiki/Ratio_test). Így
`lim_(n->oo) "sup"abs(frac{a_(n+1)}{a_n})=lim_(n->oo) "sup" frac{2}{n+1}=0<1`.
Az is igaz, hogy `sum_(n=1)^(oo) frac{2^n}{n!}=e^2-1`.
a.) sor esetén is használható a hányadoskritérium, amely szintén abszolút konvergens, így konvergens lesz. `lim_(n->oo) "sup"abs(frac{a_(n+1)}{a_n})=`
`=lim_(n->oo) "sup" frac{(n+2)n^n}{(n+1)(n+1)^(n+1)} le lim_(n->oo) "sup" frac{(n+2)}{n^2}=0<1`.
Igaz a `sum_(n=1)^(oo) frac{n+1}{n^n} approx 2,919` becslés is.
`lim_(n->oo) "sup"abs(frac{a_(n+1)}{a_n})=lim_(n->oo) "sup" frac{2}{n+1}=0<1`.
Az is igaz, hogy `sum_(n=1)^(oo) frac{2^n}{n!}=e^2-1`.
a.) sor esetén is használható a hányadoskritérium, amely szintén abszolút konvergens, így konvergens lesz. `lim_(n->oo) "sup"abs(frac{a_(n+1)}{a_n})=`
`=lim_(n->oo) "sup" frac{(n+2)n^n}{(n+1)(n+1)^(n+1)} le lim_(n->oo) "sup" frac{(n+2)}{n^2}=0<1`.
Igaz a `sum_(n=1)^(oo) frac{n+1}{n^n} approx 2,919` becslés is.
Módosítva: 3 éve
1
-
kormosmate2: Úgy gondolom ezt egy kicsit több lépésben is le lehetett volna vezetni. Az a) példában lévő felső becslés pedig kissé így a semmiből lett előhúzva különösebb magyarázat nélkül. Én értem, de a kérdező aki ezt most tanulja valószínűleg kevésbé jártasabb ebben a témában. 3 éve 0
-
gyula205: Igazad lehet. Nem ismerem olyan kristály tisztán az emelt szintű matek érettségi követelményeit és gyerekek jártasságait. Ha kell, még utólag módosíthatjuk ezt a láncszemet is. Mindenesetre köszönöm a megjegyzésedet.. 3 éve 0
-
kormosmate2: Emelt érettségin ezt nem kérdezik, ez egyértelműen egyetemi anyag, csak a kérdező nem jó kategóriában írta ki a kérdést. A kérdező minden feladat ugyannak a ZH-nak egy része. Felismertem volt tanárom feladatait bennük, 1. féléves analízis. 3 éve 0
 kormosmate2
válasza
kormosmate2
válasza
Mindkét példára alkalmazható két féle konvergencia kritérium is.
Cauchy-féle gyökkritérium: Vesszük a sorozat n-edik gyökét, majd számoljuk a határértékét, ennek az eredménye fog dönteni (vagy nem):
`lim_(n->infty) |root(n){a_n}| = {( > 1, \text{divergens}), (=1, \text{inkonklúzív}), ( < 1,\text{konvergens}):}`
D'Alambert-féle hányadoskritérium: Vesszük a sorozat n+1-edig és az általános tagjának hányadosát, majd számoljuk a határértékét, ennek az eredménye fog dönteni (vagy nem):
`lim_(n->infty) |a_{n+1}/a_n| = {( > 1, \text{divergens}), (=1, \text{inkonklúzív}), ( < 1,\text{konvergens}):}`
Az itt látható két példában lévő sorok pozitív tagúak, így az abszolútértéktől most eltekinthetünk.
a) Ha gyökkritériummal csináljuk, akkor a képen látható szorzatra átírt kifejezés határértékét keressük. Az n-edik gyökös részt Rendőr-elvvel tudjuk számolni, alulról és felülről is úgy becsüljük, hogy nevezetes határértékekre visszavezethető kifejezéseket kapjunk (`lim_(x->infty) root(n){a}=lim_(x->infty)root(n){n}=1`). Alsó becslésnél elhagyjuk belül az 1-et, felső becslésnél pedig az 1 helyére egy nagyobb kifejezést, n-t írunk. Mivel a két határérték eredménye 1, és ez közrefogja az eredetit is, a gyökös kifejezés 1-hez tart. `1/n` értelemszerűen 0-hoz tart. Így az egész határértéke 1*0=0, ami kisebb mint 1, tehát konvergens lesz a sor.
Ha hányadoskritériummal csináljuk, akkor mivel törteket osztunk, rögtön felírjuk úgy, hogy az osztandó reciprokával szorzunk. Az első törtben az exponenciális részt hatványazonosság miatt, a faktoriális részt pedig azért tudjuk úgy átírni, mert, ha `n! = n*(n-1)*...*2*1`, akkor `(n+1)! = (n+1)*n*(n-1)*...*2*1 = (n+1)*n!` Egyszerűsítés után, és a törtek átrendezése után, egy exponenciális és egy racionális tört kifejezést kapunk. Az exponenciális rész visszavezethető nevezetes határértékre (`lim_(x->infty) (1+1/n)^n=e`), így ez a rész `1/e`-hez tart, a racionális törtes rész, mivel a nevező fokszáma nagyobb mint a számlálóé, pedig 0-hoz. Az egész szorzat így 0-hoz tart, ami kisebb mint 1, tehát ugyanazt kaptuk, mint az előbb, hogy konvergens.
b) Ha a gyökkritériumot használjuk, akkor felhasználva azt a nevezetes határértéket, hogy `lim_(n->infty)root(n){n!} = infty`, akkor hamar megkapjuk, hogy a sorozat 0-hoz tart, ami kisebb mint 1, így ez a sor is konvergens.
Ha a hányadoskritériumot használjuk, akkor az előhöz példához nagyon hasonló átalakításokat követve most egy egyszerűbb törthöz jutunk, erről már könnyen látszik, hogy a határértéke 0, tehát az eredmény nyilván ugyanaz mint a másikkal.
Cauchy-féle gyökkritérium: Vesszük a sorozat n-edik gyökét, majd számoljuk a határértékét, ennek az eredménye fog dönteni (vagy nem):
`lim_(n->infty) |root(n){a_n}| = {( > 1, \text{divergens}), (=1, \text{inkonklúzív}), ( < 1,\text{konvergens}):}`
D'Alambert-féle hányadoskritérium: Vesszük a sorozat n+1-edig és az általános tagjának hányadosát, majd számoljuk a határértékét, ennek az eredménye fog dönteni (vagy nem):
`lim_(n->infty) |a_{n+1}/a_n| = {( > 1, \text{divergens}), (=1, \text{inkonklúzív}), ( < 1,\text{konvergens}):}`
Az itt látható két példában lévő sorok pozitív tagúak, így az abszolútértéktől most eltekinthetünk.
a) Ha gyökkritériummal csináljuk, akkor a képen látható szorzatra átírt kifejezés határértékét keressük. Az n-edik gyökös részt Rendőr-elvvel tudjuk számolni, alulról és felülről is úgy becsüljük, hogy nevezetes határértékekre visszavezethető kifejezéseket kapjunk (`lim_(x->infty) root(n){a}=lim_(x->infty)root(n){n}=1`). Alsó becslésnél elhagyjuk belül az 1-et, felső becslésnél pedig az 1 helyére egy nagyobb kifejezést, n-t írunk. Mivel a két határérték eredménye 1, és ez közrefogja az eredetit is, a gyökös kifejezés 1-hez tart. `1/n` értelemszerűen 0-hoz tart. Így az egész határértéke 1*0=0, ami kisebb mint 1, tehát konvergens lesz a sor.
Ha hányadoskritériummal csináljuk, akkor mivel törteket osztunk, rögtön felírjuk úgy, hogy az osztandó reciprokával szorzunk. Az első törtben az exponenciális részt hatványazonosság miatt, a faktoriális részt pedig azért tudjuk úgy átírni, mert, ha `n! = n*(n-1)*...*2*1`, akkor `(n+1)! = (n+1)*n*(n-1)*...*2*1 = (n+1)*n!` Egyszerűsítés után, és a törtek átrendezése után, egy exponenciális és egy racionális tört kifejezést kapunk. Az exponenciális rész visszavezethető nevezetes határértékre (`lim_(x->infty) (1+1/n)^n=e`), így ez a rész `1/e`-hez tart, a racionális törtes rész, mivel a nevező fokszáma nagyobb mint a számlálóé, pedig 0-hoz. Az egész szorzat így 0-hoz tart, ami kisebb mint 1, tehát ugyanazt kaptuk, mint az előbb, hogy konvergens.
b) Ha a gyökkritériumot használjuk, akkor felhasználva azt a nevezetes határértéket, hogy `lim_(n->infty)root(n){n!} = infty`, akkor hamar megkapjuk, hogy a sorozat 0-hoz tart, ami kisebb mint 1, így ez a sor is konvergens.
Ha a hányadoskritériumot használjuk, akkor az előhöz példához nagyon hasonló átalakításokat követve most egy egyszerűbb törthöz jutunk, erről már könnyen látszik, hogy a határértéke 0, tehát az eredmény nyilván ugyanaz mint a másikkal.
1
- Még nem érkezett komment!
 gyula205
válasza
gyula205
válasza
Az első ablakban a.) példa kidolgozása kiegészítésre szorul.
Felhasználjuk azt az állítást, ha `a/b ge 0` és `b > d >0`, akkor `a/b le a/d`.
`lim "sup"` belüli kifejezéseket tekintve, kapjuk a következőket:
`abs(frac{a_(n+1)}{a_n})=frac{frac{n+2}{(n+1)^(n+1)}}{frac{n+1}{n^n}}
=frac{(n+2)n^n}{(n+1)*(n+1)^(n+1)} le frac{(n+2)*n^n}{(n+1)*n^(n+1)}=`
`=frac{(n+2)}{(n+1)*n} le frac{n+2}{n^2}<1`, ha `n>2`.
Az első egyenlőtlenségnél a nevező második tényezőjében a hatványalapot becsüljük `(n+1) > n`-vel, míg a másodiknál a nevező első tényezőjét ugyanezzel.
Felhasználjuk azt az állítást, ha `a/b ge 0` és `b > d >0`, akkor `a/b le a/d`.
`lim "sup"` belüli kifejezéseket tekintve, kapjuk a következőket:
`abs(frac{a_(n+1)}{a_n})=frac{frac{n+2}{(n+1)^(n+1)}}{frac{n+1}{n^n}}
=frac{(n+2)n^n}{(n+1)*(n+1)^(n+1)} le frac{(n+2)*n^n}{(n+1)*n^(n+1)}=`
`=frac{(n+2)}{(n+1)*n} le frac{n+2}{n^2}<1`, ha `n>2`.
Az első egyenlőtlenségnél a nevező második tényezőjében a hatványalapot becsüljük `(n+1) > n`-vel, míg a másodiknál a nevező első tényezőjét ugyanezzel.
Módosítva: 3 éve
1
- Még nem érkezett komment!