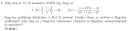Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Paraméteres függvény
 ZS0fi19
kérdése
ZS0fi19
kérdése
309
Sziasztok! A lenti feladatban szeretnék segítséget kérni, hogy hogyan kell megoldani. Nagyon megköszönném, ha érthetően levezetné valaki, mert így könnyebben tudom megérteni az ilyen típusú feladatokat.
Jelenleg 1 felhasználó nézi ezt a kérdést.
#matematika, #függvény, #Paraméter
#matematika, #függvény, #Paraméter
0
Középiskola / Matematika
Válaszok
1 kormosmate2
megoldása
kormosmate2
megoldása
Mellékelt képeken a megoldás.
Szöveges kiegészítés:
Az, hogy a P(1,2) ponton áthalad a függvény görbéje (azaz, hogy ez a pont rajta van), azt jelenti, hogy az 1-hez a 2-t rendeli a függvény, így ennek megfelelően kell kiszámolni A értékét. Ha ez megvan, akkor elkezdünk vizsgálódni.
Zérushelyből kettő is van, ezeket akkor kapjuk, ha csak a számlálóban előforduló zárójelek 0-k. Ebből az egyik kétszeres is, azaz páros multiplicitású. Ez azt jelenti, hogy a függvény ezen a helyen az x tengelyt, csak visszagörbülve fogja értinteni valamelyik oldalról. A másik, aminek páratlan multiplicitása van, keresztezi az x tengelyt ezen a helyen.
Hézagpontja nincs a függvénynek, ehhez kellenének olyan zárójelek, amelyek a tört mindkét részében előfordulnak.
Pólushelyből is kettő van, ezeket akkor kapjuk, ha csak a nevezőben előforduló, vagy mindkét helyen de a nevezőben magasabb hatványon előforduló zárójelek 0-k. Ezeken a helyeken van függőleges aszimptotája a függvénynek. Az egyik itt is páros multiplicitású, azaz mindkét irányból ugyanabba a végtelenbe (mindkétfelől fölfelé vagy lefelé) fog tartani, még a másiknál ellentétes ellőjelű végtelenekhez. Hogy pontosan mely végtelenekbe, azt határérték számításokkal kapjuk.
Először megnézzük az ellentétes előjelűt. Mivel végig szorzás van, a törtből "leválasztjuk" a "problémás" részt, ez okozza a szakadást ebben a pontban. Megvizsgáljuk a jobb és a bal oldali határértéket is ebben a pontban. Azt kell nézni, hogy a nevező a 0-t pozitív, vagy negatív számokon keresztül éri-e el, ezt utána annak megfelelően jelöljük. A többi részbe csak simán behelyettesítjük a -1/2-et, és kapunk egy számot. A legvégén a szorzásnál figyelni kell az előjelekre. 1/-0 "eredménye" -végtelen, de ha ez utána egy negatív számmal szorzódik, akkor már pozitív végtelen kapnánk. Most pozitív számmal szorzunk, így marad a negatív végtelen.
Ugyanezt csináljuk határértékkel 3-ban is, itt viszont felesleges a két oldali határérték, mert a négyzet miatt a nevezőben a 0-t így is úgy is pozitív számokon keresztül közelítjük.
Végül meg kell még néznünk a határértékeket a két végtelenben is, hogy tudjuk, "jobbra és balra" hová tart a függvény. Amit rögtön látunk még minden előtt, hogy ez a függvény egy áltört, mivel a számláló és nevező fokszáma megegyezik (mindkettő 3-ad fokú). Így az eredmény mindkét esetben egy szám lesz, tehát egy vízszintes aszimptotánk lesz majd. Ahhoz, hogy ezt a számot kiderítsük, nem kell a rengeteg algebrát elvégezni, mivel az ilyen polinomos törtes határértékeknél elég csak a számláló és a nevező "legerősebb" tagjait nézni. Képzeljük el, hogy elkezdenénk felbontani a zárójeleket, felül biztosan lenne egy `x^3`, minden más szorzat csak ettől kisebb fokszámú. Nevezőben hasonlóan lesz egy `2x^3` a többi ettől kisebb, és így nem fognak számítani, mert "eltörpülnek" a végtelenben. Innen már látható, hogy ami marad, az 1/2-hez fog tartani.
Végül a pontosabb rajz érdekében kiszámolhatjuk még, hogy a függvény hol metszi az y tengelyt, azaz 0-ban mi a helyettesítési értéke.
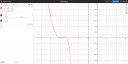
Ezzel kiderítettünk mindent ami kellett a vázlatos ábrához, a 3.,4. képeken látható a függvény grafikonja, bal oldalon a fekete körös sorokban pedig az aszimptoták egyenletei. A 4. képet azért tettem be, mert az elsőn szinte egyáltalán nem látszódnak jól a zérushelyek, mert a függvénynek ezen a részen nagyon közeli értékei vannak. Elég durván szét kell nyújtani az y tengely mentén az ábrát, hogy látszódjon a két zérushely szépen.
Szöveges kiegészítés:
Az, hogy a P(1,2) ponton áthalad a függvény görbéje (azaz, hogy ez a pont rajta van), azt jelenti, hogy az 1-hez a 2-t rendeli a függvény, így ennek megfelelően kell kiszámolni A értékét. Ha ez megvan, akkor elkezdünk vizsgálódni.
Zérushelyből kettő is van, ezeket akkor kapjuk, ha csak a számlálóban előforduló zárójelek 0-k. Ebből az egyik kétszeres is, azaz páros multiplicitású. Ez azt jelenti, hogy a függvény ezen a helyen az x tengelyt, csak visszagörbülve fogja értinteni valamelyik oldalról. A másik, aminek páratlan multiplicitása van, keresztezi az x tengelyt ezen a helyen.
Hézagpontja nincs a függvénynek, ehhez kellenének olyan zárójelek, amelyek a tört mindkét részében előfordulnak.
Pólushelyből is kettő van, ezeket akkor kapjuk, ha csak a nevezőben előforduló, vagy mindkét helyen de a nevezőben magasabb hatványon előforduló zárójelek 0-k. Ezeken a helyeken van függőleges aszimptotája a függvénynek. Az egyik itt is páros multiplicitású, azaz mindkét irányból ugyanabba a végtelenbe (mindkétfelől fölfelé vagy lefelé) fog tartani, még a másiknál ellentétes ellőjelű végtelenekhez. Hogy pontosan mely végtelenekbe, azt határérték számításokkal kapjuk.
Először megnézzük az ellentétes előjelűt. Mivel végig szorzás van, a törtből "leválasztjuk" a "problémás" részt, ez okozza a szakadást ebben a pontban. Megvizsgáljuk a jobb és a bal oldali határértéket is ebben a pontban. Azt kell nézni, hogy a nevező a 0-t pozitív, vagy negatív számokon keresztül éri-e el, ezt utána annak megfelelően jelöljük. A többi részbe csak simán behelyettesítjük a -1/2-et, és kapunk egy számot. A legvégén a szorzásnál figyelni kell az előjelekre. 1/-0 "eredménye" -végtelen, de ha ez utána egy negatív számmal szorzódik, akkor már pozitív végtelen kapnánk. Most pozitív számmal szorzunk, így marad a negatív végtelen.
Ugyanezt csináljuk határértékkel 3-ban is, itt viszont felesleges a két oldali határérték, mert a négyzet miatt a nevezőben a 0-t így is úgy is pozitív számokon keresztül közelítjük.
Végül meg kell még néznünk a határértékeket a két végtelenben is, hogy tudjuk, "jobbra és balra" hová tart a függvény. Amit rögtön látunk még minden előtt, hogy ez a függvény egy áltört, mivel a számláló és nevező fokszáma megegyezik (mindkettő 3-ad fokú). Így az eredmény mindkét esetben egy szám lesz, tehát egy vízszintes aszimptotánk lesz majd. Ahhoz, hogy ezt a számot kiderítsük, nem kell a rengeteg algebrát elvégezni, mivel az ilyen polinomos törtes határértékeknél elég csak a számláló és a nevező "legerősebb" tagjait nézni. Képzeljük el, hogy elkezdenénk felbontani a zárójeleket, felül biztosan lenne egy `x^3`, minden más szorzat csak ettől kisebb fokszámú. Nevezőben hasonlóan lesz egy `2x^3` a többi ettől kisebb, és így nem fognak számítani, mert "eltörpülnek" a végtelenben. Innen már látható, hogy ami marad, az 1/2-hez fog tartani.
Végül a pontosabb rajz érdekében kiszámolhatjuk még, hogy a függvény hol metszi az y tengelyt, azaz 0-ban mi a helyettesítési értéke.
Ezzel kiderítettünk mindent ami kellett a vázlatos ábrához, a 3.,4. képeken látható a függvény grafikonja, bal oldalon a fekete körös sorokban pedig az aszimptoták egyenletei. A 4. képet azért tettem be, mert az elsőn szinte egyáltalán nem látszódnak jól a zérushelyek, mert a függvénynek ezen a részen nagyon közeli értékei vannak. Elég durván szét kell nyújtani az y tengely mentén az ábrát, hogy látszódjon a két zérushely szépen.
Módosítva: 3 éve
1
- Még nem érkezett komment!