Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Matek
 nagyaliz
kérdése
nagyaliz
kérdése
1754
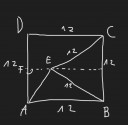
ABCD négyzet oldalának 12 egység van megadva hosszként. Gondoljunk arra, hogy a négyzet belsejében ki van jelölve az E pont, úgy, hogy BE = CE = 12 egység. Számítsd ki az A és az E távolságát!
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Középiskola / Matematika
Válaszok
1 kormosmate2
megoldása
kormosmate2
megoldása
Mellékeltem ábrát.
1. megoldás: Kössük össze az A csúcsot az E-vel. Ekkor `ABEangle+EBCangle = 90^circ`. Mivel `BECtriangle` szabályos, így `EBCangle = 60^circ`, és így `ABEangle = 30°`. Innen `AE` számolható koszinusz tétellel, de mivel `ABEtriangle` egyenlőszárú, így a háromszög elfelezésével számolhatjuk egy sima szinusszal is a keresett oldal felét. Én most az előbbit fogom alkalmazni:
`AE^2=12^2+12^2-2*12^2*cos 30^circ approx 38.58 Rightarrow AE approx 6.21`.
2. megoldás: Az `EBCtriangle` E csúcsból húzott magasságvonala egyben a háromszög felezőegyenese is, mivel a háromszög szabályos. Felezőegyenes lévén ez a szakasz mindkét másik oldaltól, és így a B és C csúcsoktól is azonos távolságra van. De ez egyúttal azt is jelenti, hogy ha ezt a vonalat meghosszabbítjuk az `AD` oldalig, akkor ez éppen a négyzet középvonala lesz, tehát a `BC` és `AD` oldalt is pontosan felezi, utóbbit az ábrán jelölt F pontban. Így felezéssel és Pitagorasz tétellel, vagy a szabályos háromszög magasságára vonatkozó összefüggést használva, a magasság: `m=12*sqrt{3}/2 = 6\sqrt{3}`
A négyszög középvonala párhuzamos a négyzet 2 oldalával, és hossza megyegyezik velük, azaz 12 a hossza. Így `FE = 12-6\sqrt{3} approx 1.61`. Mivel `AFEtriangle` derékszögű, a keresett oldal innen Pitagorasz tétellel számolható: `AE=\sqrt{6^2+1.61^2} approx 6.21`.
1. megoldás: Kössük össze az A csúcsot az E-vel. Ekkor `ABEangle+EBCangle = 90^circ`. Mivel `BECtriangle` szabályos, így `EBCangle = 60^circ`, és így `ABEangle = 30°`. Innen `AE` számolható koszinusz tétellel, de mivel `ABEtriangle` egyenlőszárú, így a háromszög elfelezésével számolhatjuk egy sima szinusszal is a keresett oldal felét. Én most az előbbit fogom alkalmazni:
`AE^2=12^2+12^2-2*12^2*cos 30^circ approx 38.58 Rightarrow AE approx 6.21`.
2. megoldás: Az `EBCtriangle` E csúcsból húzott magasságvonala egyben a háromszög felezőegyenese is, mivel a háromszög szabályos. Felezőegyenes lévén ez a szakasz mindkét másik oldaltól, és így a B és C csúcsoktól is azonos távolságra van. De ez egyúttal azt is jelenti, hogy ha ezt a vonalat meghosszabbítjuk az `AD` oldalig, akkor ez éppen a négyzet középvonala lesz, tehát a `BC` és `AD` oldalt is pontosan felezi, utóbbit az ábrán jelölt F pontban. Így felezéssel és Pitagorasz tétellel, vagy a szabályos háromszög magasságára vonatkozó összefüggést használva, a magasság: `m=12*sqrt{3}/2 = 6\sqrt{3}`
A négyszög középvonala párhuzamos a négyzet 2 oldalával, és hossza megyegyezik velük, azaz 12 a hossza. Így `FE = 12-6\sqrt{3} approx 1.61`. Mivel `AFEtriangle` derékszögű, a keresett oldal innen Pitagorasz tétellel számolható: `AE=\sqrt{6^2+1.61^2} approx 6.21`.
Módosítva: 3 éve
0
-
kormosmate2: Ez egyébként egy középszintű érettségi feladat volt még 2019 májusában. 3 éve 1