Mateek

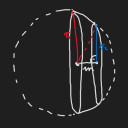
Csatolt képen a vizsgált test ábrája. Ha jól értelmezem, akkor a sugár 3/4-ét a gömb közepétől kell számítani. Ennek a testnek a palástját gömbövnek hívjuk, felszíne ` A = 2pi*R*m `, ahol R az eredeti, szeletelés nélküli gömb sugara, azaz a főkör sugara (ami most az ` r_1 `), m pedig a gömböv magassága. Ehhez még hozzájön a két fedőkör területe is, ezekre rendre ` r_1^2pi ` és ` r_2^2pi `. Az egész kimetszett testet gömbrétegnek hívjuk, térfogata ` V=(pi*m)/6(3r_1^2+3r_2^2+m^2) `.

` r_1 ` az átmérő fele, azaz ` 35/2 ` cm. ` m ` értéke a feladat szövege alapján: elfelezzük az átmérőt, majd annak vesszük a 3/4-t, így ` m=35/2*3/4 = 105/8 ` cm. Nem tudjuk még az ` r_2 `-t. A képen látható ábrán berajzoltam még egy szaggatott piros vonalat is. Így egy derékszögű háromszöget kapunk a gömbréteg belsejében. A szaggatott piros vonal hossza megegyezik ` r_1 `-el, hiszen a gömb felszínének minden pontja ugyanolyan távolságra van a középpontjától. Innen Pitagorasz tétellel: ` r_2=\sqrt{(35/2)^2-(105/8)^2} = \sqrt{8575/64} = \sqrt{8575}/8` cm.

Így a felszín: ` A=2pi*35/2*105/8+(35/2)^2pi+(8575/64)pi = 57575/64pi approx 2826.206 ` cm2

A térfogat: ` V= (pi*105/8)/6(3*(35/2)^2+3*8575/64+(105/8)^2) = 1672125/512\pi approx 10260.0305` cm3

2. kérdés. Gömb térfogata: ` V= 4/3r^3pi `. Így kiszámítandó:

` 4/3r^3pi = 1672125/512\pi Rightarrow r^3= 5016375/2048 Rightarrow r= \root(3){5016375/2048} approx 13.48 ` cm