Valaki tudna segíteni ebben a feladatban?

15,

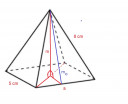
Ez rajzzal indítunk, azon sokmindent észrevehetünk. Rajzolunk egy négyzet alapú gúlát és felírjuk mellé, amit ismerünk. Alapéle 5 cm, oldaléle 8 cm.

a,

A térfogatának kiszámításához érdemes tudni a magasságát, mert a gúla térfogata:

`V_("gúla")=(a^2*m)/3` ; ahol 'a' az alapél és 'm' a magasság.

A magasságot nem ismerjük, keresünk derékszögű háromszöget, amiből ki tudjuk számolni. Amint az ábrán is látható, a gúla alapjának félátlója, az oldaléle és a magassága egy derékszögű háromszöget alkot; a félátlót ki tudjuk számolni.

`("Átló")/2` = `a*root()(2)/2` = `5/2*root()(2)` cm

Most jöhet Pitagorasz, a két befogó a félátló és a magasság; az átfogó pedig az oldalél.

`o^2=(("Átló")/2)^2+m^2`

ebből kifejezzük m-et:

`m=root()(o^2-(("Átló")/2)^2)` = `root()(8^2-(5/2*root()(2))^2)` = `root()(64-50/4)` = `root()(103)/2` `approx` 7,18 cm

A gúla (gyertya) térfogata:

`V_("gúla")=(a^2*m)/3` = `(5^2*7.18)/3` = `ul("60 " cm^3)`.

b,

130 db ilyen gyertya térfogata:

`V=130*V_("gúla")` = `130*60` = 7800 `cm^3`

Ezen felül még van 6 % veszteség. Az elkészített gyertyák térfogata a 100 %, mi pedig kiszámoljuk, mennyi a 106 %.

100 % felel meg 7800 `cm^3`-nek

106 % megfelel `106/100*7800` = 8268 `cm^3`-nek.

A feladat literben kéri a megoldást, vagyis ez `ul("8,3 liter")`.

c,

Ehhez a részhez szükségünk van a gúla felszínére. Ehhez meg kell határoznunk a gúla oldallapjának magasságát (`m_o`, az ábrán kékkel jelölve).

Megint derékszögű háromszöget keresünk. A derékszögű háromszög befogói a testmagasság (m) és az alapél fele (`a/2`), átfogója az oldallap magassága.

`m_o^2=m^2+(a/2)^2` = `7.18^2+2.5^2` = 57,8

`m_o` = 7,6 cm

A gúla felszíne:

`A_("gúla")` = `T_("alap")+T_("palást")` = `a^2+4*(a*m_o)/2` = `5^2+2*5*7.6` = 101 `cm^2`

40 db gúla felszíne:

`A=40*A_("gúla")` = `40*101` = 4040 `cm^2`

A csomagolóanyag ennek a felületnek a 136 %-a, vagyis:

`4040*1.36` = ul("5494 " cm^2)`.