Az A csúcsból induló súlyvonal a B és C csúcsok között húzódik, és a háromszög súlypontjának koordinátáit adja. A háromszög súlypontja a következőképpen számítható: ((-4+2+6)/3; (6+-4+5)/3) = (2;3). A B csúcsból induló magasságvonal a C és A csúcsok között húzódik, és a metszéspont koordinátái az egyenes egyenletei alapján számíthatók. A háromszög területe a Heron-formula alapján számítható: √(s(s-a)(s-b)(s-c)) ahol s a háromszög oldalhosszának összege és a,b,c az oldalak hosszai.

Az egyenes egyenlete az irányvektor szerint v(x,y) = (3,4) * t és A(2,6) és B(15,-6) két pontjának egyenlete f(x,y) = (x-2)/13 = (y-6)/(-12) = t . A két egyenlet együttes megoldása adja a metszéspont koordinátáit.

Egyenes normálvektoros egyenlete: ` Ax+By=Ax_0+By_0 ` ahol ` \vec{n}(A,B) ` egy az egyenesre merőleges normálvektor, `(x_0,y_0) ` pedig egy az egyenesen lévő pont. (Természetesen van több mód is két ponton átmenő egyenes egyenletének a felírása, de most használjuk ezt, mert most ezzel később egyszerűbb lesz)

1) Háromszög súlyvonala a csúcsot a szemközti oldal felezőpontjával összekötő egyenes. Az A csúcsból induló súlyvonal másik pontja a BC oldal felezőpontja: ` F((2+6)/2;(-4+5)/2) = F(4;1/2)`. Ekkor az A pontból az F-be mutató vektor: ` \vec{AF}(4-(-4);1/2-6) = (8;-11/2) `(végpont-kezdőpont koordinátái). Ez a vektor párhuzamos a kérdéses egyenessel (azaz az irányvektora), ezért forgassuk el 90°-al, ekkor egy normálvektorát kapjuk. Ezt úgy tehetjük meg, hogy megcseréljük a két koordinátáját, és az egyiket megszorozzuk (-1)-el. Így ` \vec{n}(11/2;8) `. A normálvektornak csak az iránya a lényeges, a hossza nem számít, így a kétszerese is megfelel, hogy ne legyenek törtek, tehát: ` \vec{n}(11;16) `

Ekkor a súlyvonal egyenlete, az A pontot felhasználva:
` 11x+16y=11*(-4)+16*6 Rightarrow 11x+16y = 52`

A magasságvonal hasonló elvvel, azzal a különbséggel, hogy most nincs csak egy pontunk. A B csúcsból induló magasságvonal viszont merőleges az AC egyenesre, így az A-ból C-be mutató vektor épp a kérdéses egyenes normálvektora lesz: ` \vec{AC}(6-(-4);5-6) = \vec{n}(10;-1) `

A magasságvonal egyenlete így:
` 10x-y=10*2+(-1)*(-4) Rightarrow 10x-y=24 `

A két egyenes metszéspontjához a két egyenes egyenletéből álló egyenletrendszert kell megoldanunk.

A fejezzük ki a másodikból ` y `-t, ` (y=10x-24) ` majd írjuk be az első egyenletbe és oldjuk meg:

` 11x+16(10x-24)=52 `

` 11x+160x-384=52 `

` 171x-384=52 \text{/}+384`

` 171x=436 \text{/}:171`

` x= 436/171 `

Így ` y = 10(436/171)-24 = 256/171 `.

Tehát a metszéspont koordinátái: ` M(436/171;256/171) `

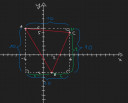
A háromszög területét legegyszerűbben a csatolt képen illusztrált módon lehet számolni. Az egész háromszög befoglalható egy 10*10-es négyzetbe. Ennek a területéből kivonjuk a három kisebb, derékszögű háromszög területét, és ami marad az a háromszög területe. A szükséges hosszok leolvashatóak az ábráról. Így a háromszög területe: ` T_triangle = 10^2-((10*1)/2+(9*4)/2+(10*6)/2) = 47 `

2) Az e egyenes átmegy az origón, és az irányvektora ` \vec{v}(3;4) ` ami azt jelenti, hogy a meredeksége ` 3/4 `. Így az e egyenes egyenlete: ` e: y=3/4x `

A másik egyenes az előző feladatban látott módon. ` \vec{AB}(15-2;-6-6) = \vec{AB}(13;-12) `
Így az f egyenes normálvektora: ` \vec{n}(12;13) `. Tehát az f egyenes egyenlete, az A pontot használva:
` f: 12x+13y=12*2+13*(-6) Rightarrow f: 12x+13y = -54 `

A metszéspont kiszámítása szintén az előző feladat mintájára. Írjuk be az első egyenletet a másodikba:
` 12x+13(3/4x)=-54 `

` 12x+39/4x=-54 \text{/}*4 `

` 48x+39x=-216 `

` 87x=-216 \text{/}:87 `

` x=-72/29 `

Így ` y= 3/4*(-72/29) = -54/29 `

Tehát a két egyenes metszéspontjának koordinátái: ` e\cap f: M(-72/29;-52/29) `