Az eredeti gúla térfogatát a magassága alapján kiszámíthatjuk a 3/4πR^3 képlettel, ahol R az alapgömb sugara. A csonka gúla térfogatát pedig a kérdésben adták, ez 336 cm^3.
A csonka gúla felszíne pedig a teljes felszín és a alaplap különbsége, tehát 4/3πR^3 és πR^2.

A csonka gúla oldallapjai az alaplap síkjával bezárt szöge a csonka gúla magasságának és a csonka gúla alapél hosszának aránya.
A magasság az eredeti gúla alapél harmada, a hossz pedig az eredeti gúla alapél felezőpontja.

Csatoltam képet.

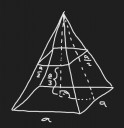
Első képen a gúla ábrája. Legyen az alapél hossza: ` a `. A fedő négyzet éleinek hossza az alapél fele `a/2 `, hiszen ezek a palástot alkotó háromszögek középvonalai. A magasság pedig a feladat szövege alapján: ` a/3 `. Ismert a keletkezett csonkagúla térfogata. A csonkagúla térfogata: ` V=m/3(T+\sqrt{T*t}+t) `, ahol m a magassága, T és t pedig rendre az alap-; és fedőlap területe. Így:
` (a/3)/3(a^2+\sqrt{a^4/4}+a^2/4) = a/9(a^2+a^2/2+a^2/4) = a/9*(7a^2)/4 = (7a^3)/36 = 336 Rightarrow a^3=1728 Rightarrow a=12`

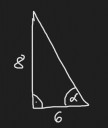
Így az eredeti gúla magassága ` 2*a/3 = 8 `, a fedőlap élei pedig 6. A második képen az első képen a gúla belsejébe rajzolt derékszögű háromszög látható, ahol a hosszabbik befogó az eredeti gúla magassága. A másik befogó azért 6, mert az éppen az alapnégyzet középvonalának a fele. Ennek a háromszögnek az átfogója Pitagorasz tétellel: ` \sqrt{8^2+6^2} = \sqrt{100}=10 `, ami éppen az eredeti gúla palástot alkotó háromszögeinek a magassága.
Szabályos gúla lévén, a palástot alkotó négy háromszög mind ugyanolyan, továbbá középvonaluk a magasságukat felezi, így a palástot alkotó trapézok magassága 5. A csonkagúla felszíne így: alapnégyzet+fedőnégyzet+a négy palástot alkotó trapéz területe. Azaz:

` A = 12^2+6^2+4*(12+6)/2*5 = 360` cm2

A 2. kérdésben a második képen látható derékszögű háromszögben az ` alpha ` szög a kiszámítandó. Ez egy sima tangensel kijön: ` \text{tg }alpha = 8/6=4/3 Rightarrow alpha=53.13^circ `