Az eredeti gúla térfogatát a magassága alapján kiszámíthatjuk a 3/4πR^3 képlettel, ahol R az alapgömb sugara. A csonka gúla térfogatát pedig a kérdésben adták, ez 336 cm^3.
A csonka gúla felszíne pedig a teljes felszín és a alaplap különbsége, tehát 4/3πR^3 és πR^2.

A csonka gúla oldallapjai az alaplap síkjával bezárt szöge a csonka gúla magasságának és a csonka gúla alapél hosszának aránya.
A magasság az eredeti gúla alapél harmada, a hossz pedig az eredeti gúla alapél felezőpontja.

Csatoltam képet.

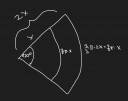
Az első képen a kiterített palást és az azt kiegészítő körcikk a középponti szöggel. Ezen ` x `-el jelöltem a kisebb sugarat. Ekkor a rövidebb és a hosszabb ívhossz is ráírható az ábrára, mert ívhossz=középponti szög (radiánban)*sugár. Továbbá a feladatban mindent végig radiánban fogok számolni, ` 120^circ = 2/3\pi `.

A képen látható síkidom megfeleltethető egy körcikknek. Körcikk területe=középponti szög*sugár^2/2, a körgyűrű területét pedig úgy kapjuk, hogy nagyobb körcikk területéből kivonjuk a kisebbiket. Így

` (2/3\pi*(2x)^2)/2-(2/3\pi*x^2)/2=200 Rightarrow (2/3\pi*3x^2)/2 = 200 Rightarrow x^2*pi = 200 Rightarrow x = \sqrt{200/\pi} `

Így a hosszabbik ív hossza: ` 4/3\pi*x = 4/3pi*\sqrt{200/pi}`
A rövidebbik ív hossza: ` 2/3\pi*x = 2/3pi*\sqrt{200/pi}`

Ezek éppen rendre a csonkakúp alap és fedőkörének a kerületei. Innen a sugaruk számolható:

` R=1/(2\pi)*4/3pi*\sqrt{200/pi} = 2/3*\sqrt{200/pi} = 2*\sqrt{200/(9pi)}`

` r= 1/(2\pi)*2/3pi*\sqrt{200/pi} = 1/3*\sqrt{200/pi} = \sqrt{200/(9pi)}`

A térfogathoz kelleni fog még a test magassága.

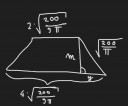
A második képen a csonkakúp tengelymetszete látható. Ez egy trapéz, amelynek a két szára (ami egyben a kúp alkotója) ` x ` hosszúságú, az alapok pedig az alap-; és fedőkörök átmérői (azaz a sugarak kétszeresei). A szimmetria miatt, az ` y `-al jelzett hossz=(trapéz alsó alapja-trapéz felső alapja)/2, azaz:

` y=1/2*(4*\sqrt{200/(9pi)}-2\sqrt{200/(9pi))) = \sqrt{200/(9pi)}`

Az ` m `-et ekkor számolhatjuk Pitagorasz tétellel:

` m = \sqrt{200/pi-200/(9pi)} = \sqrt{1600/(9pi)} = 40/(3\sqrt{pi})`

Csonkakúp térfogata: ` V=\frac{pi*m}{3}(R^2+R*r+r^2) `

Tehát: ` V=\frac{pi*40/(3\sqrt{pi})}{3}(800/(9pi)+400/(9pi)+200/(9pi)) = \frac{40*1400}{81\sqrt{pi}} = \frac{56000}{81\sqrt{pi}}` cm3